

 |
 |
|
Факторинг Анализ финансовых западных рынков Поскольку значения R/S - случайные переменные, нормально распределенные, можно было бы ожидать, что значения Н также будут нормально распределенными. В таком случае ожидаемая дисперсия показателя Херста была бы следующей: Уаг(Н)п=1Л (5.7) где Т = общее количество наблюдений в выборке Это было бы дисперсией вокруг Е(Н)п, как рассчитано из E(R/S)n. Обратите внимание, что Var(H)n не зависит от п или Н, но, вместо этого, зависит от полного объема выборки Т. Еще раз повторим, что эксперименты методом Монте-Карло проводились для проверки истинности уравнения (5.7). Для нормально распределенной случайной переменной, дважды перемешанной, 7 ООО значений Н были рассчитаны для 10 < п < 50. Моделирование было проведено для Т = 200, 500, 1 ООО и 5 ООО. Результаты приведены в Таблице 5.3: 1. Средние значения Н соответствуют Е(Н) с использованием значений E(R/S) из уравнения (5.6), показывая, что эмпирическая поправка к формуле Эниса и Ллойда обоснованна. 2. В каждом случае дисперсия очень близка к 1/Т. Таблица 53 Стандартное отклонение Е(Н): 10 < п < 50
Моделирование было повторено для 10 < п < 500, 10 <= п <= 1000 и 10 < п < 5000. В каждом случае Е(Н) соответствовало значению, предсказанному уравнением (5.6), и дисперсия приблизительно равна 1/Т. На основании результатов таблицы 5.1 мы можем сказать, что Е(Н) для IID случайных переменных может быть рассчитано из уравнения (5.6), с дисперсией 1/Т. На рисунке 5.5 показаны нормализованные распределения для различных значений Т. Как и ожидалось, они оказываются нормально распределенными. Что, если независимый процесс отличается от гауссова процесса? Как мы видели в таблице 5.2, независимое распределение с толстыми хвостами и высоким пиком действительно обнаруживает средние значения, как они были предсказаны в уравнении (5.6). Тем не менее, дисперсия все-таки отличается. К сожалению, дисперсия для распределений, которые не являются нормально распределенными, отличается на индивидуальном основании. Поэтому наш доверительный интервал имеет силу только для 1Ю случайных переменных. Существуют, конечно, способы отфильтровывания краткосрочной зависимости, и в дальнейшем мы будем использовать эти методы. >> о с 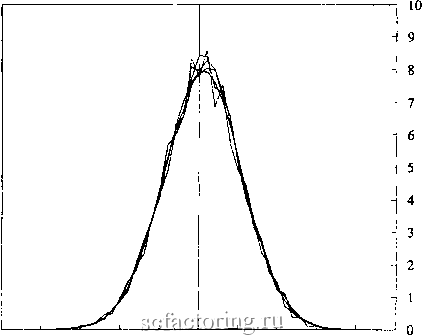 -5 -4 -3-2-10 1 2 Standard Deviations РИСУНОК 5.5 Е(Н) для 10 <п <50, нормализованная частота: Т = 500,1000,5000,10000. В следующем разделе исследуется R/S-анализ различных типов временных рядов, которые часто используются в моделировании финансовой экономики, а также другах видов стохастических процессов. Особое внимание будет уделяться возможности ошибки второго рода (классификация процесса как имеющего долговременную память, тогда как в действительности, процесс имеет кратковременную память). СТОХАСТИЧЕСКИЕ МОДЕЛИ Для финансовых временных рядов были предложены пять основных типов процессов с кратковременной памятью: 1. Авторегрессионные процессы (AiR); 2. Процессы скользящего среднего (МА); 3. Авторегрессионные процессы скользящего среднего (ARMA); 4. Авторегрессионные интефированные процессы скользящего среднего (ARIMA); 5. Авторегрессионные условные гетероскедастические процессы (ARCH). Каждый из этих процессов имеет ряд вариантов, которые являются улучшениями основных моделей. Эти улучшения пытаются приблизить характеристики временного ряда к фактическим данным. Мы исследуем каждый из этих процессов по очереди, но основное внимание будет уделено основным моделям. Варианты основных моделей будут оставлены для будущего исследования. Кроме того, Мандельбротом (1964, 1972, 1982) был предложен процесс с долговременной памятью, названный дробным броуновским движением. Изучение дробного броуновского движения будет отложено до Главы 13. В таблице 5.4 подводятся итоги следующего раздела. Таблица 5.4 R/S -анализ стохастических процессов
* Обобщенный авторегрессионный условный гетероскедастический процесс. Авторегрессионные процессы Авторегрессионный процесс - это процесс, в котором изменение переменной в некоторой точке времени является линейно коррелированым с предыдущим изменением. Вообще, корреляция уменьшается экспоненциально со временем и исчезает за относительно короткий период. Отсюда следует общая форма: Cn = en + a*Cn-, + b*Cn-2 (5.8) где Сп = изменение С во времени п, О < С < 1 а, Ь = константы с а < 1, Ь < 1 е = ряд белого шума со средним О и дисперсией сг Уравнение (5.8) является авторегрессионным процессом порядка 2, или AR(2), поскольку изменение во времени п связано, с изменением в последние два периода. Процесс AR(q) возможен там, где изменение С во времени п зависит от предыдущих q периодов. Для проверки вероятности процесса AR строится регрессия там, где изменение во времени п является зависимой переменной, и изменения в предыдущие q периоды (задержки) используются как независимые переменные. Для каждой задержки оценивается t-статистика. Если любые t-статистики существенны на 5-процентном уровне, то мы можем сформулировать гипотезу о том, что работает AR-процесс. Офаничения диапазона значений для коэффициентов
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||