\A/V

РИСУНОК 62 Функция Вейерштрасса.

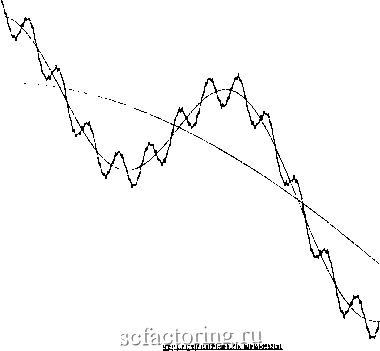-iO.5

iLIJUUI!lliilllilL:lll.aiJI<ltIlttJIJil!a: ! I

РИСУНОК 63 функция Вейерштрасса, первые четыре частоты.

График в логарифмическом масштабе по обеим осям для R/S-анализа показан на рисунке 6.4. Конец каждого частотного цикла и начало следующего ясно видны как разрывы или уплощения на фафике R/S. Заметьте, что наклон для каждой частоты также понижается. Для самой короткой частоты Н = 0,95; для самой длинной частоты Н = 0,72. Часть фафика R/S для второй самой короткой частоты включает в начале шишку . Эта шишка - появление более короткой предыдущей частоты. В третьей самой короткой частоте неясно видны две шишки. Однако к третьей частоте наложение самоафинной структуры слишком зазубрено, чтобы можно было различить меньшие структуры. Это приводит нас к заключению, что R/S-анализ может различить циклы внутри циклов, если количество циклов меньше четырех. При большем количестве циклы становятся размазанными. Если бы было бесконечное количество циклов, как в полной функции Вейерштрасса, то фафик в логарифмическом масштабе по обеим осям был бы прямой линией с Н ~ 0,70.

0.5 1 1.5 2 2.5 3 3.5 4

Log(Number of Observations)

РИСУНОК 6.4 R/S-aiiaiH3, функция Вейерштрасса.

Есть более легкий способ увидеть, когда в фафике в логарифмическом масштабе по обеим осям появляются разрывы, и лучше оценить продолжительность цикла. Следующая простая статистика первоначально использовалась Херстом (Hurst, 1951) для проверки на стабильность. Я также нашел, что она дает более точное измерение длины цикла, которое особенно хорошо работает в присутствии шума. Эта статистика, называемая V-статистикой, определяется следующим образом:

Vn = (R/S)n/V (6.3)

Это отношение приведет к горизонтальной линии, если R/S статистика изменяет масштаб пропорционально квадратному корню из времени. Другими

i 1-5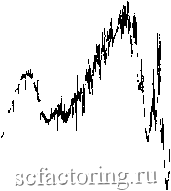

>

1.5 2 2.5 3 Log(Number of Observations)

РИСУНОК 63 Фунюдия Вейерштрасса, V-статистика.

НЕПЕРИОДИЧЕСКИЕ ЦИКЛЫ

Непериодический цикл не имеет абсолютной частоты. Вместо нее он имеет среднюю частоту. Мы знакомы со многими процессами, которые имеют абсолютные частоты, и они имеют тенденцию быть большими, очень важными системами. Они включают время, необходимое для одного оборота Земли вокруг солнца, а также время, необходимое нашей планете, чтобы совершить один оборот вокруг своей оси.

словами, фафик V против log(n) будет плоским, если процесс является независимым, вероятностным процессом. С другой стороны, если процесс персистентен и R/S изменяет масштаб быстрее, чем квадратный корень из времени (Н > 0,50), то фафик будет иметь наклон вверх. Наоборот, если процесс антиперсистентен (Н < 0,50), фафик будет иметь наклон вниз. При вычерчивании V на оси у и log(n) на оси X разрывы появятся, когда фафик V выравнивается. В таких точках процесс с долговременной памятью рассеивается.

На рисунке 6.5 показана V-статистика для уравнения Вейерштрасса. Обратите внимание на сглаживание наклона в конце каждого периодического цикла. Исследуя максимальное значение V в каждом интервале, мы можем оценить длину цикла для каждой частоты. Из рисунка 6.5 мы можем видеть, что R/S-анализ способен определять периодические циклы, даже когда они накладываются. Но у нас есть для этого другие инструменты. Реальной силой R/S-анализа является обнаружение непериодических циклов.