б.Нахождение циклов; периодических и непериодических

смоделировано в электронной таблице. Начиная с лага п = 50, шаги таковы:

1. Вставьте 0,10 в ячейку А1. Скопируйте 0,10 в первые 50 ячеек в столбце А.

2. В ячейке А51, напечатайте: 0,9*А50 + .2*А1.

3. Скопируйте ячейку А51 вниз для 8 ООО ячеек.

При изменении лага п введите 0,10 для первых п ячеек в столбце А. Выполните вышеуказанные действия, начиная шаг 2 в ячейке А(п + 1).

На рисунке 6.7 показаны первые 500 из 8 ООО наблюдений, используемых для этого испытания. Обратите внимание на нерегулярные длины цикла, типичные для нелинейной динамической системы. На рисунке 6.8 представлен график R/S для всех 8 ООО значений с очевидным Н = 0,93 для п < 50. Однако при п > 50 наклон является фактически нулевым, показывая, что достигнут максимальный диапазон. Уравнение Макки-Гласса, будучи гладкой, детерминированной системой, имеет показатель степени Херста близкий к 1. На рисунке 6.9 приведен фафик V-статистики для тех же значений. Длина цикла при приблизительно 50 наблюдениях абсолютно очевидна. На рисунке 6.10 отставание было изменено на 100 наблюдений. Разрыв фафика R/S теперь происходит при п = 100, подтверждая тот факт, что R/S-анализ может обнаруживать различные длины цикла. Читателю советуется изменить отставание уравнения Макки-Гласса, чтобы проверить это заключение.

м .1

II I

I I I

1. 1 1

I , 1,

500 1000

Number of Observations

1500

РИСУНОК 6.7: Уравнение Макки-Гласса: отставание наблюдения = 50.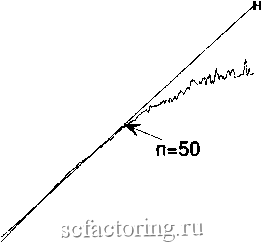

=0.93

О ........-------------.....

0.5 1 1.5 2 2.5

Log(Number of Observations)

РИСУНОК 6.8 R/S-анализ, уравнение Макки-Гласса: отставание наблюдения = 50.

а :

22 I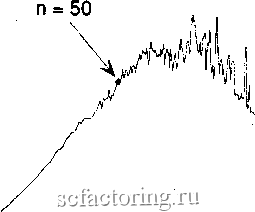

>

3.5 3

-\ 2

-t 1.5

\ 1 ] 0.5

1 1.5 2 2.5

Log(Number of Observations)

РИСУНОК 6.9 V-статистика, уравнение Макки-Гласса: отставание наблюдения = 50.

п = 100

, , 1.5

0.5 1 1.5 2 2.5 3 3.5 4 Log(Number of Observations)

РИСУНОК 6.10 RyS-анализ, уравнение Макки-Гласса: отставание наблюдения = 100.

Добавление шума

Рисунок 6.8 показывает, что R/S-анапиз может определить среднюю длину непериодических циклов для большого значения Н. Однако многие испытания очень хорошо работают в отсутствии шума, но при добавлении небольшого количества шума процесс терпит неудачу. Примеры включают сечения Пуанкаре и реконструкцию фазового пространства. Тем не менее, поскольку R/S-анализ был создан для измерения количества шума в системе, можно было бы ожидать, что R/S-анализ будет более устойчивым к шуму.

Существует два типа шума в динамических системах. Первый называется наблюдаемым или аддитивным шумом. Этот шум не затрагивает систему; вместо этого шум представляет проблему для измерения. Наблюдатель испытывает затруднения при точном измерении выхода системы, так что к зарегистрированному значению прибавляется шумовое приращение.

Например, предположим, что вы изучаете капающий кран, измеряя время между каплями. Вы установили измерительный прибор на столе и поместили микрофон под тем местом, куда капает вода, чтобы записать точный момент, когда капля воды ударяется о дно. К сожалению, вы находитесь в оживленной лаборатории, где много других людей, которые также выполняют эксперименты. Каждый раз, когда кто - то проходит мимо, ваш стол немного покачивается, и это изменяет время, когда капля ударяется о микрофон. Аддитивный шум является внешним для процесса. Это проблема наблюдателя, а не системы.

К сожалению, когда большинство людей думает о шуме, они думают об аддитивном шуме. Однако второй тип шума, называемый динамическим шумом,