

 |
 |
|
Факторинг Анализ финансовых западных рынков В данный момент интуитивно может быть проведена связь с рынками. Рынки могут быть в местном масштабе случайны, но они имеют глобальную статистическую структуру, которая является неслучайной. Таким образом, традиционная количественная теория тлела бы тенденцию поддерживать локальную случайность. Испытания на эффекгавность рынка долго сосредотачивались на том, могут ли фаткосрочные прогнозы быть сделаны с достаточной точностью, чтобы принести прибыль. Как правило, юшичественные исследования показывали, что трудно получить прибыль от 1фаткосрочного (недельного или меньшего) оживления на рынке. Тем не менее, удлинение нашего горизонта времени, как оказывается, улучшает нашу прогнозирующую способность. ЧТО ТАКОЕ ФРАКТАЛ? Мы еще не определили термин фрактал . Фактически не существует точного определения. И даже математика, самый лаконичный из всех языков, испытывает затруднения при описании фракгала. Это подобно вопросу, сформулированному Глубокой Мыслью в Путеводитаче путешествующего автостопом по Гашктике Дугласа Адамса. Глубокая Мысль - суперкомпьютер, созданный высшей расой, чтобы ответить на последний вопрос жизни, вселенной и всего . Глубокая Мысль дает ответ (ответ - 42 ), но никто не знает, как задать вопрос таким образом, чтобы ответ мог быть понят. Это похоже на фракталы. Мы узнаем их, когда мы их видим, но мы испытываем трудности, описывая их с достаточной точностью для того, чтобы понять полностью, что они собой представляют. Бенуа Мандельброт (Benoit Mandelbrot), отец фрактальной геометрии, тоже не сформулировал точного определения. Фракгалы действительно имеют определенные особенности, которые измеримы, и свойства, которые являются желательными для целей моделирования. Первое свойство, сачоподобие, уже было описано довольно подробно. Оно означает, что части в некотором роде связаны с целым. Это подобие может быть точным , как в треугольнике Серпинского, где каждый маленький треугольник геометрически идентичен большому треугольнику. Такая точная форма самоподобия существует только математически. В действительности, самоподобие качественно ; то есть объект или процесс являются подобными в различных масштабах, пространственных или временных, статистически. Каждый масштаб напоминает ;фугие масштабы, но не идентичен им. Отдельные ветви дерева качественно самоподобны другим ветвям, но каждая ветвь также является уникальной. Это свойство самоподобия делает фрактал масштабно-инвариантным: он испытывает недостаток в характерном масштабе, из которого происходят другие. Логарифмическая спираль, которая играет заметную роль в теории волн Эллиотта, является одним из примеров характеристической функции масштаба. Раковина моллюска кораблик - логарифмическая спираль, потому что спираль сохраняет свои исходные пропорции по мере увеличения размера. Поэтому кораблик растет, но не меняет свою форму, потому что он растет в соагветствии с характерной пропорцией - он обладает характерной масштабной чертой. Логарифмическая спираль не является фрактальной. Теория волн Эллиотта также таковой не является. Аналогично, ранние модели объяснения строения легкого млекопитающих основывались на экспоненциальном механизме масштабирования. В частности, диаметр каждого поколения ответвлений должен уменьшаться примерно на один и тот же коэффициент от одного поколения к следующему. Если z представляет номер поколения, а средний диаметр поколения ответвлений z, то: d, = q*d,.,d (1.1) Вайбель и Гомес (Weibel and Gomez, 1962) оценили, что q = 2 так что уравнение (1.1) может быть переписано как: d, = d(,*2- (1.2) где do = диаметр трахеи (главный отдел легкого) Таким образом, эта модель имеет характерный масштабный коэффициент, q=2 . Каждое поколение ответвлений постепенно уменьшается, в соответствии с точным коэффициентом, аналогично тому, как уменьшалось предыдущее поколение. Это характерный масштаб. Уравнение (1.1) может быть переписано в более общей форме: d.rdoe- (1.3) где а = -ln(q) > О Как утверждают Уэст, Уэлмик и Гольдбергер (West, Valmik, Goldberger, 1986): Таким образом, если единственный параметр а характеризует этот прюцесс, то d (z,a) интерпретируется как средний диаметр в поколении z для масштабного коэффициента а . Отметьте экспоненциальную форму уравнения (1.3) с использованием характерного масштаба. Тем не менее, моделирование легкого, основанное на характерном масштабе, игнорирует прочие свойства. В пределах каждого поколения фактические диаметры имеют диапазон: некоторые больше, а некоторые меньше среднего числа. Кроме того, экспоненциальный закон подобного преобразования соответствует только первым десяти поколениям ответвлений. Помимо этого, существует систематическое отклонение от характерной функции масштаба. Рисунок 1.2 взят из работы Уэста и Гольдбергера (West and Goldberger, 1987). Если уравнение (1.3) остается в силе, то график диаметра в логарифмическом масштабе против номера поколения должен образовать прямую линию. Наклон этого графика в логарифмическом масштабе только по одной оси должен быть коэффициентом масштабирювания. Мы можем видеть, что экспоненциальная особенность масштабирования не захватывает всю форму легкого. Однако фафик в логарифмическом масштабе по обеим осям (Рис. 1.3), использующий логарифм номера поколения, действительно приводит к волнистой линии, которая отклоняется вправо. Но что означает график в логарифмическом масштабе по обеим осям? 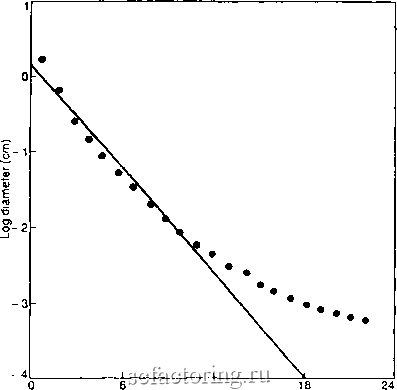 Generation (z) РИСУНОК 1.2 Легкое с экспоненциальным масштабированием. (Из работы Уэста и Гольдбергера (West and Goldberger, 1987). 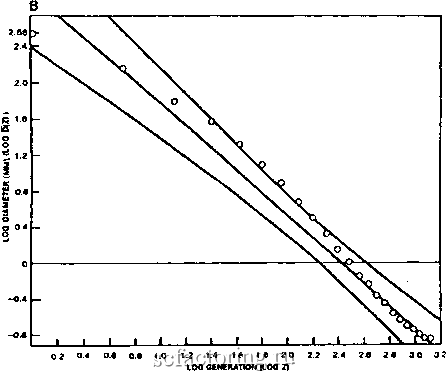 РИСУНОК 13 График в логарифмическом масштабе по обеим осям
|