

 |
 |
|
Факторинг Анализ финансовых западных рынков
Pound 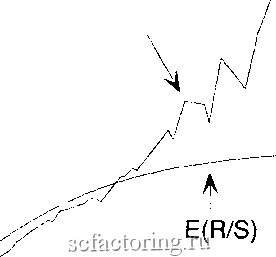 0.5 1 1.5 2 2.5 3 Log(Number of Days) РИСУНОК 123 V-статистика, фунт, дневные данные, январь 1972 г.-декабрь 1990 г. ИЕНА/ФУНТ Курс иена/фунт немного отличается от других обменных курсов. Япония и Великобритания не являются главными торговыми партнерами: торговля валютой, происходящая между ними, намного менее активна. Кроме того, форвардный рынок, где происходит большая часть хеджирования валюты, котируется в обменных курсах доллара США. Таким образом, обменный курс иена/фунт не котируется непосредственно, а выводится из отношения обменного курса иена/доллар и обменного курса фунт/доллар. В результате обменный курс иена/фунт выглядит чрезвычайно случайным в периоды короче 100 дней. Другие обменные курсы имеют схожие характеристики, но обменный курс иена/фунт фактически идентичен случайному блужданию на более высоких частотах. Рисунок 12.4 показывает, как близко V-статистика следует за своим ожидаемым значением в течение периода менее 100 дней. Даже при том, что обменный курс иена/фунт не привлекает большого внимания, он также не имеет очевидной длины цикла. Долговременная память либо чрезвычайно длинна, либо бесконечна.
Yen/Pound 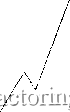 E(R/S) 0.9 08 1 1.5 2 2.5 3 3.5 4 Log(Number of Days) РИСУНОК 12.4 V-статистика, иена/фунт, дневные данные, январь 1972 г. - декабрь 1990 г. ВЫВОДЫ Валюта имеет интересные статистические и фундаментальные характеристики, которые отличают ее от других процессов. По существу, валюта не является ценной бумагой, хотя в отношении нее осуществляется активная торговля. Крупнейшие участники, центральные банки не представляют собой максимизаторов доходности; их цели не обязательно соответствуют целям рациональных инвесторов. В то же время на рьшках валюты мало признаков циклов, хотя они действительно имеют сильные тренды. На основании этих характеристик, взятых вместе, мы полагаем, что валюта -истинный процесс Херста. То есть она характеризуется процессами бесконечной памяти. Долгосрочные инвесторы должны опасаться относиться к валюте так, как они относятся к другим торговым объектам. В частности, они не должны предполагать, что стратегия с покупкой и длительным владением будет выгодна в долгосрочной перспективе. Риск увеличивается во времени и не уменьшается со временем. Долгосрочному инвестору, который должен иметь валютный риск, следует рассмотреть активную торговлю такими активами. Они не предлагают никакого преимущества в долгосрочной перспективе. ЧАСТЬ 4 fРАКТАЛЬНИЙ ШУМ Дробный шум и R/S-анализ в предыдущих главах мы видели доказательства того, что рынки, по крайней мере, в краткосрочной перспективе, являются персистентными процессами Херста, а волатильность, статистический побочный продукт, антиперсистентна. Гипотеза фрактального рынка предлагает экономическое объяснение наблюдаемых самоподобных распределений вероятности, но она не предлагает математическую модель для исследования ожидаемого поведения. В этой и следующих главах мы рассмотрим такие модели. Они должны согласовываться с гипотезой фрактального рынка, описанной в Главе 3. Мы видели, что краткосрочные рыночные прибыли производят самоподобные распределения частот, характеризующиеся высоким пиком в среднем и более толстыми хвостами, чем при нормальтюм распределении. Это может быть процесс, связанный с ARCH или GARCH. Как отмечено в Главе 4, ARCH образуется коррелированными условными дисперсиями. Прибыли все еще независимы, поэтому некоторая форма ЕМН еще будет иметь силу. Однако мы также видели в Части 2, что рынкч характеризуются показателями Херста более 0,50, что подразумевает долговременную память в прибылях, в отличие от процессов GARCH и ARCH, которые были исследованы в Главе 4. Кроме того, мы нашли, что дисперсия не является персистентным процессом; наоборот, она антиперсистентна. Основываясь на R/S-анапнзс, ни процесс ARCH, ни его производные не соответствуют пе{х-истентност н или эффектам долговременной памяти, которые характеризуют рынки. Следовательно, нам нужна альтернативная статистическая модель, которая имеет распределения с толстыми хвостами, проявляет персистентность и имеет нес габильныс дисперсии. Cyui,ecTByei класс шумовых процессов, который соответствует этим критериям: 1/Г или дробные П1умы. В отличие от процесса ARCH, который зависит от сложной стагистчсской чшшпуляции, дробные njyMbi представляют собой обоби1ение iipouecc()i5 броу1Ювского движения. Кажется, что они ]ювсюду. Повсеместная природа 1/Гн]ума озадачивала и интриговала ученых в течение некоторого времени, l/f-шум особенно характерен для фазовых переходов, где внутренние масштабы длины или времени прск-ращают существовать; то есть корреляции становятся бесконечными.
|