

 |
 |
|
Факторинг Анализ финансовых западных рынков будет временем релаксации для этого фактора. Рааличные акции, вероятно, будут оценивать информацию разными темпами. Поэтому рынок в целом будет иметь много различных параллельных времен релаксации в качестве реакции на одну и ту же информацию. Согласно гипотезе фрактального рынка более вероятно, что различные инвесторы с различными инвестиционными горизонтами реагируют на информацию многократными временами релаксации; то есть информация затрагивает различных инвесторов по-разному в зависимости от их инвестиционного горизонта. Поэтому волатильность, которая является мерой неуверенности на рынке, подверглась бы многим параллельным изменениям с различными временами корреляции или релаксации. Шрёдер (Schroeder, 1991) предложил формулу для моделирования l/f-шума, и она является более надежной, чем метод трех ифальных костей Восса. Она задействует генератор процессов релаксации. Эта формула повторяется для уровней частоты, равноотстоящих в логарифмическом пространстве, и суммируется. Формула проста и может быть легко реализована компьютерами, даже в электронной таблице. Формула такова: Хп+1=Р*Хп + (13.2) гдехо = 0 г = равномерное случайное число р = желаемое время корреляции р связано со временем релаксации t следующим отношением: p = exp(-l/t) (13.3) где t - время релаксации. Выбираются три значения t, равноотстоящих в логарифмическом пространстве, и генерируются три ряда х. Например, если желаемая последовательность находится в пространстве logio, используется t = 1, 10 и 100. Будут получены значения р = 0,37, 0,90 и 0,99 соответственно. Шрёдер говорит, что три наблюдения, равноотстоящие в логарифмическом пространстве, являются достаточными для хорошей аппроксимации. В этом случае частоты отделены степенями 10. В случае с игральными костями это были степени 2. Тем не менее, важно обратить внимание на то, что это - аппроксимация. Теоретически, l/f-шум состоит из бесконечного числа таких процессов релаксации, происходя параллельно на всех различных частотах. Чем больше частот мы добавляем к моделированию, тем лучше результаты. Уравнение (13.2) может быть легко смоделировано в электронной таблице, с использованием следующих шагов: 1. Поместите столбец, состоящий из приблизительно 1 ООО случайных чисел, в столбце А. 2. В ячейке В1 поместите 0. 3. В ячейку В2 поместите следующее уравнение: 0.37*В 1 + @sqrt(l - 0,37 л 2) *А2 4. Скопируйте ячейку В2 вниз для 1 ООО ячеек. 5. Повторите шаги 1 - 4 в столбцах С и D, но в шаге 3 замените 0,37 на 0,90. 6. Повторите шаги 1 - 4 в столбцах Е и F, но в шаге 3 замените 0,37 на 0,99. 7. Сложите столбцы А, С и F в столбце G. В столбце G содержится розовый шумовой ряд. Постройте график этого ряда и сравните его со случайным. Заметьте, что в нем много более крупных изменений, как положительных, так и отрицательных, а также больше частых инверсий. Уравнение (13.2) выглядит очень простым, но между его частями происходит комплексное взаимодействие. Первый член в правой части - простой процесс AR(1), подобный тем, которые мы исследовали в Главе 4. Следовательно, это уравнение содержит бесконечную память, как и процессы AR(1). Однако мы также видели в Главе 4, что системы AR(1) персистентны для коротких временных интервалов. Как мы увидим, этот ряд является антиперсистентным. Что-то во втором члене должно вызывать антиперсистентность. Второй член - случайный шок. Его коэффициент обратно пропорционально связан с коэффициентом корреляции в первом члене. Например, когда р = 0,37, коэффициент при втором члене составляет 0,93; а когда р = 0,90, коэффициент при втором члене равен 0,43. То есть, чем сильнее процесс AR(1), тем менее сильным является случайный шок. Однако случайный шок входит в процесс AR при следующей итерации и становится частью процесса бесконечной памяти. Случайный шок удерживает систему от достижения равновесия. Если бы случайный элемент пе был включен, каждый ряд х достиг бы равновесия ко времени релаксации t. Однако случайный элемент продолжает возмущать систему; она гюстоянрю меняет направление и никогда не успокаивается. Можно ожидать, что такой тип системы будет иметь неустойчивую дисперсию и среднее. Мы исследуем эту проблему более подробно в Главе 14. На рисунке 13.1 показан график в логарифмическом масп1табе по обеим осям спекгральной функции против частоты для ряда из 1 ООО наблюдений, созданных согласно уравнению (13.2). Наклон линии - 1,63, что дает b = 1,63 или Н = 0,31 согласно уравнению (13.1). На рисунке 13.2 приведен R/S-анализ того же ряда. R/S-анализ дает Н = 0,30, подтверждая уравнение (13.1). Значения изменяются, потому что уравнение (13.1) дает асимптотическое значение Н. Для небольшого числа наблродений значения R/S будут смещены и будут следовать за ожидаемыми значениями из уравнения (5.6). Однако оба результата находятся в близком соответствии. Что еще более важно, оба дают антиперсистентные значения Н. Они выглядят очень похожими на исследования волатильности в Главе 9. о Он, ей о 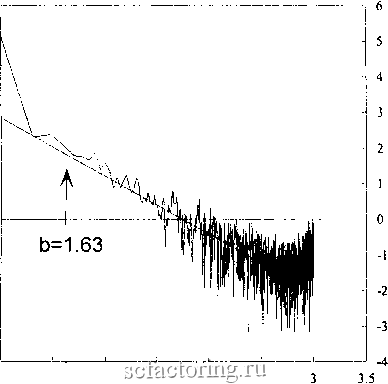 1 1.5 2 2.5 Log(Frequency) РИСУНОК 13.1 Спектральные функции, l/f-uiyivi: алгоритм многократной релаксации. E(R/S) Relaxation Process Н=0.30 - 1.6 1.5 1.4 Н 1.3 1,2 1.1 1 0.9 0.8 0.7 0,6 0.5 0.4 1 1.5 2 2.5 LogCNumber of Observations) РИСУНОК 13.2 R/S-анализ, антиперсистентность: процесс релаксации.
|