

 |
 |
|
Факторинг Анализ финансовых западных рынков следовали семь лет голода. Эффект Иосифа представлен суммированием степенного закона в уравнении (13.9). Эффект Ноя Как показано на рисунке 6.6, уравнение (13.9) производит следы времени с соответствующим значением Н или необходимым количеством зазубренности; то есть оно дублирует фрактальную размерность следа времени и эффект Иосифа или долговременной памяти. Черный шум имеет дополнительную характеристику: катастрофы. Уравнения (13.8) и (13.9) не вызывают катастрофы, потому что они являются дробными гауссовыми шумами. Они объясняют только один аспект черного шума: долговременную память. Normal 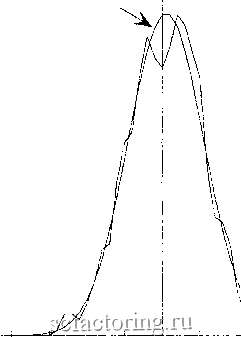 Fractional Noise 7 Н=0.72 , -4 -3-2-10 1 2 Standard Deviations РИСУНОК 13.6 Частотное распределение, дробный шум: Н = 0,72. Черный шум также характеризуется разрывами в проекции прямой времени: на ней существуют резкие прерывистые движения вверх и вниз. Эти прерывистые катастрофы приводят к появлению высоких пиков в среднем и толстых хвостов в частотном распределении процессов черного шума. Мандельброт (Mandelbrot, 1972) назвал это свойство эффектом Ноя, памятуя о библейской истории о потопе. На рисунке 13.6 показано частотное распределение изменений для FBM, использованное для создания рисунков 6.6(a) и (Ь). Этот ряд имеет Н = 0,72, согласно R/S-анализу, и его частотное распределение подобно нормальному гауссову шуму. Мы можем видеть (1), что алгоритмы имитации FBM не обязательно охватывают все ожидаемые характеристики, и (2) один большой недостаток R/S-анализа: R/S-аиализ не может различить дробные гауссовы шумы и дробные негауссовы шумы. Поэтому недостаточно одного R/S-анализа, чтобы сделать выюд о том, что система представляет собой черный шум. Нам также нужно частотное распределение с высоким пиком и толстыми хвостами. Даже в этом случае есть третья юзможность шумового хаоса, который мы исследуем более подробно в Части 5. Эффект Ноя, важный аспект черного шума, часто не замечается, потому что он добавляет еще один уровень сложности к анализу. Это происходит, потому что более крупные события устиваются в системе; то есть происходит что-то, что вызывает итерированный контур обратной связи, очень подобно логистическому уравнению. Однако в логистическом уравнении катастрофы происходили часто, также как и в процессах розового шума. В черном шуме они случаются менее часто; система остается персистентной, вместо того чтобы стать антиперсистентной. Статистически, кажется, что мы не способны воспроизвести эффект Ноя путем моделирования. Однако мы можем воспроизвести его, как мы увидим в нелинейной динамике. ЗЕРКАЛЬНЫЙ ЭФФЕКТ Розовые шумы и черные шумы обычно имеют место в природе, но есть ли между ними взаимосвязь? Обязательно ли обнаружение одного приведет к другому? В спектре l/f-шумов это вполне могло бы иметь место. Мандельброт и Ван Несс (Mandelbrot and Van Ness, 1968), так же как и Шрёдер (Schroeder, 1991), показали, что коричневый шум - подынтефальное выраисение белого шума; то есть коричневый шум представляет собой просто текушую сумму белого шума. Из этого также следует, что производная или скорость коричневого шума является белым шумом. Следовательно, в l/f-спектре ряд белого шума может быть легко переведен в коричневый шум через некоторый тип зеркального эффекта. В уравнении (13.1) спекфальный показатель b бьш эквивалентен 2*Н + 1. Мы таюке упоминали, что для производной FBM спекфальный показатель составляет 2*Н - 1. Таким образом, персистентный ряд с 0,50 < Н < 1,00 будет иметь спектральный показатель больше 2,0, сигнализируя о процессе черного шума. Однако производная процесса черного шума будет иметь b < 1,0, делая его процессом розового шума. Поэтому не удивительно, что волатильность курсов ценных бумаг на фондовом рынке является антиперсистентной. Рыночные прибьши представляют собой процесс черного шума, поэтому их ускорение или волатильность должны быть, как мы обнаружили, процессом розового шума. Мы также подтвердили, что неправильно говорить о том, что рыночные прибьши подобны турбулентности , которая является известным процессом розового шума. Употреблять этот неправильный термин - все равно, что говорить о том, что движущаяся вода является турбулентной. Турбулентность, которую мы измеряем, является не самой жидкостью, а скоростью жидкости. Аналогично, турбулентность рынка заключается в скорости изменений цен, а не в самих изменениях. В качестве дальнейшего испытания взаимосвязи розового и черного шума мы можем исследовать второе различие - изменения изменений - посредством R/S-анализа. Согласно этой взаимосвязи, если пертое различие - черный шум, то второе различие должно быть розовым шумом. На рисунке 13.7 приведен график R/S в логарифмическом масштабе по обеим осям пятидневных прибьшей по индексу Доу-Джонса для акций промышленных компаний, который использовался в Главе 8. Обратите внимание, что Н = 0,28, что совместимо с антиперсистентьшм процессом розового шума. Я нашел, что это будет верным для любого процесса с Н > 0,50. 1.5 - 0.5 - E(R/S) Н=0.58 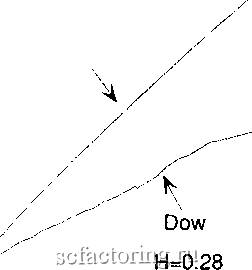 о L---- 1.5 2 2.5 3 Log(Number of Observations) РИСУНОК 13.7 R/S-анализ, индекс Доу-Джонса для акций промышленных компаний, пятидневные прибыли: второе различие. ДРОБНОЕ ДИФФЕРЕНЦИРОВАНИЕ: МОДЕЛИ ARFIMA Помимо более экзотических моделей долговременной памяти, которые мы обсуждали, существует также и обобщенная версия моделей ARIMA (авторегрессионных интегрированных моделей скользящего среднего), которые мы обсуждали в Главе 5. ARIMA-модели - гомогенные нестационарные системы, которые могут быть сделаны стационарными посредством последовательного дифференцирования наблюдений. Более общая модель ARIMA (p,d,q) могла бы также включать авторегрессионные компоненты и компоненты скользящего среднего, в смешанном виде или по отдельности. Параметр дифференцирования d всегда был значением целого числа. Хоскинг (Hosking, 1981) далее обобщил первоначальное значение ARIMA (p,d,q) для дробного дифференцирования, чтобы выработать авторегрессионный дробно интегрированный процесс скользящего среднего (ARRMA); то есть d может быть любым реальным значением, включая дробные
|