

 |
 |
|
Факторинг Анализ финансовых западных рынков f(b,*t)*f(b2*t) = f(b*t) (14.2) Следовательно, f(b*t), f(b2*t) и f(b*t) имеют распределение одинаковой формы, несмотря на то, что они являются произведениями друг друга. Этим объясняется их устойчивость . Характеристические функции Фактическое представление устойчивых распределений обьмно делается по Мандельброту (Mandelbrot, 1964) с использованием логарифма их характеристических функций: 0(t) = ln[f(t)] = ln[E(e**)] = i*5*t-c*t *(l -i*p*(t/t)*tan(7c*a/2),a 1, = i*5*t- c*t*(l + i*P*(2/7t)*lnt), a= 1 (14.3) Устойчивые распределения имеют четыре параметра: а, Р, с и 5. Каждый имеет свою собственную функцию, хотя только два являются критическими. Сначала рассмотрим относительно незначительные параметры с и 5. 5 -параметр положетт. По существу, распределение может иметь средние значения, отличные от О (стандартного нормального среднего), что зависит от 5. В большинстве случаев исследуемое распределение нормализовано, и 5 = 0; то есть среднее распределения полагается равным 0. Параметр с - масштабный параметр. Он наиболее важен при сравнении реальных распределений. Опять же, в пределах понятия нормализации параметр с походит на выборочное отклонение; он является мерой дисперсии. При нормализации выборочное среднее обычно вычитается (чтобы дать среднее равное 0) и делится на стандартное отклонение, так чтобы единицы были в терминах выборочного стандартного отклонения. Нормализация вьшолняется, чтобы сравнить эмпирическое распределение со стандартным нормальным распределением со средним равным О и стандартным отклонением равным 1. с используется, чтобы задать единицы, которыми распределение расширяется и сжимается около 5. Значение с по умолчанию равно 1. Единственная цель этих двух параметров - задать масштаб распределения относительно среднего и дисперсии. Они не являются действительно характерными для какого-либо из распределений, и поэтому они менее важны. Когда с = 1, а 5 = 0, распределение, как говорят, принимает приведенный вид. Параметры аир определяют форму распределения и чрезвычайно важны. Эти два параметра зависят от порождающего процесса; а с и 5 - нет. Р - параметр асимметрии. Он принимает такие значения, что -1 < Р < +1. Когда Р = О, распределение симметрично около 5. Когда параметр асимметрии меньше О, распределение имеет отрицательную асимметрию; когда он больше О, распределение имеет положительную асимметрию. Параметр а, характеристический показатель, определяет островершинность в § и толщину хвостов. Характеристический показатель может принимать значения О < а < 2. Когда а = 2,0, распределение является нормальным, при этом дисперсия равна Часть ф Фрактальный шум 2*с . Тем не менее, когда а < 2,0, второй момент, или дисперсия генеральной совокупности, становится бесконечным или неопределенным. Когда 1 < а < 2,0, существует первый момент, или математическое ожидание; когда а < 1, математическое ожидание также становится бесконечным. Бесконечная дисперсия и среднее Для большинства индивидуумов, которые обучены стандартной гауссовой статистике, идея бесконечных среднего или дисперсии кажется абсурдной или даже извращенной. Мы всегда можем вычислить дисперсию или среднее выборки. Как оно может быть бесконечным? Еще раз повторим, что мы применяем частный случай, гауссову статистику, ко всем случаям. В семействе устойчивых распределений нормальное распределение - частный случай, который существует, когда а = 2,0. В этом случае математическое ожидание и дисперсия действительно существуют. Бесконечная дисперсия означает, что не существует дисперсии совокупности , к которой стремится распределение в пределе. Когда мы берем выборочную дисперсию, мы делаем это, согласно гауссову предположению, как оценку неизвестной дисперсии совокупности. Шарп (Sharpe, 1963) говорил, что беты (в смысле современной теории портфеля (МРТ)) должны рассчитьшаться на основании ежемесячных данных за пять лет. Шарп выбрал пять лет, потому что этот период дает статистически значимую выборочную дисперсию, необходимую для оценки дисперсии совокупности. Пятилетний период статистически значим, только если лежащее в основе распределение является гауссовым. Если оно не является гауссовым и а < 2,0, выборочная дисперсия ничего не говорит о дисперсии совокупности, потому что дисперсии совокупности нет. Выборочные дисперсии, как ожидалось бы, будут неустойчивыми и не будут стремиться ни к какому значению, даже при увеличении объема выборки. Если а < 1,0, то же самое верно и ддя среднего, которое также не существует в пределе. Рисунки 14.1 и 14.2 показывают, как бесконечное среднее и дисперсия влияют на устойчивые распределения, используя последовательное среднее и стандартное отклонение по Фамэ (Fama, 1965b). На рисунке 14.1 использовано 8 ООО выборок из известного распределения Коши, которое имеет бесконечное среднее и дисперсию. Распределение Коши более подробно описьшается ниже. Используемый здесь ряд был нормализован путем вычитания среднего и деления на выборочное стандартное отклонение. Таким образом, все единицы выражены в стандартных отклонениях. Для сравнетшя мы используем 8 ООО гауссовых случайных переменных, которые были нормализованы аналогичным образом. Важно понять, что два последующих шага всегда будут заканчиваться в среднем О и стандартном отклонении 1, потому что они бьши нормализованы к этим значениям. Конвергенция означает, что временной ряд быстро идет к устойчивому значению. На рисунке 14.1(a) показано поачедователыюе среднее, которое вычисляет среднее, по мере того как по одному добавляются наблюдения. Для системы с конечным средним последовательное среднее будет, в конечном счете, стремиться к математическому ожиданию при использовании достаточного количества данных. В этом случае оно будет 0. На рисунке 14.1(a) временной ряд гауссовых случайных чисел сходится в пределах 0,02 стандартных отклонений среднего примерно к 500 наблюдениям. Хотя он блуждает вокруг среднего О, он делает это случайным, однородным образом. Напротив, хотя ряд Коши не отходит далеко от О, он делает это систематическим, прерывистым образом; то есть в последовательном среднем есть дискретные скачки, после которых оно начинает систематически подниматься. 0.05 I - - - Random 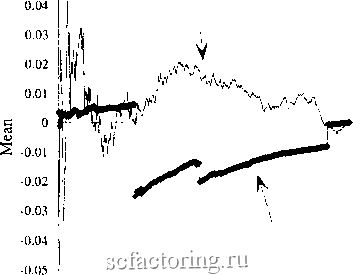 Cauchy -0.06 2 3 4 5 6 7 Thousands of Observations РИСУНОК 14.1a Конвергенция последовательного среднего, функция Коши. На рисунке 14.2(a) показано последовательное стандартное отклонение дпя тех ке двух рядов. Последовательное стандартное отклонение, подобно последовательному :реднему, является вычислением стандартного отклонения, по мере того как по одному добавляются наблюдения. В этом случае разница еще более поразительна. Случайный эяд быстро сходится к стандартному отклонению 1. Распределение Коши, напротив, тикогда не сходится. Вместо этого оно характеризуется несколькими большими трерывистыми скачками и большими отклонениями от нормализованного значения 1. На рисунке 14.1(b) приведен фафик последовательного среднего данных тятидневного индекса Доу-Джонса для акций промышленных компаний, используемых J Главе 8 и в других разделах данной книги, но оно также было нормализовано к среднему О и стандартному отклонению 1. Приблизительно после 1 ООО дней фафик сходится к значению в пределах 0,01 стандартного отклонения 0. Гауссов случайный $ременной ряд показывает схожее поведение. Среднее прибылей по индексу Доу-Д}1юнса кажется устойчивым, как можно было бы ожидать от устойчивого )рактального распределения. Это поведение однородно и непрерывно. Оно не 1роявляет дискретных скачков, обнаруженных в функции Коши с ее бесконечным ;редним.
|