0.001

0.ООО1

00OOOI

Т-1-1 111111-1-I-I I 1 м i

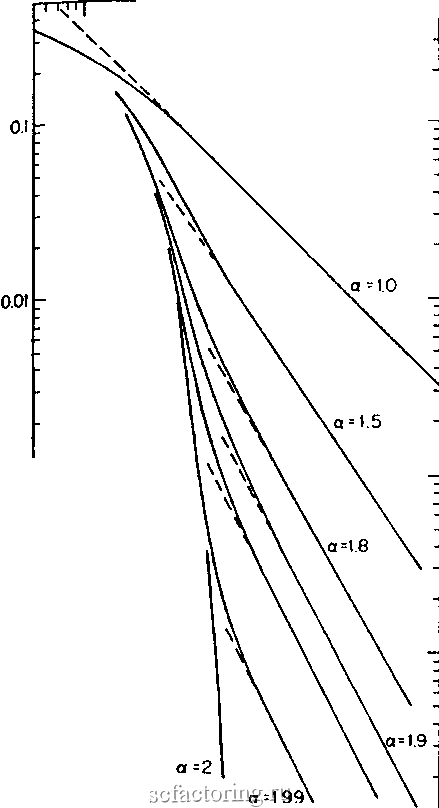Mill I I ..... 1

a =195 J-[ t I 111

РИСУНОК 14.4 График в логарифмическом масштабе по обеим осям для различных значений а. (Из работы Мандельброта OMandelbrot, 1964).

log(P(U, > u)) = - a*log(u) - log(U,)) log(P(U2 < u)) = - a*logu - logCU.))

(14.7a) (14.7b)

Уравнения (I4.1a) и (14.7b) - для положительных и отрицательных хвостов соответственно. Эти уравнения подразумевают, что наклон графика в логарифмическом масштабе по обеим осям должен асимптотически иметь наклон, равный - а. Принятый метод вьшолнения этого анализа состоит в том, чтобы составить фафик частоты в логарифмическом масштабе по обеим осям в положительном и отрицательном хвосте против абсолютного значения частоты. Когда хвост достигнут, наклон должен быть приблизительно равен а, в зависимости от размера выборки. Рисунок 14.4 взят из работы Мандельброта (Mandelbrot, 1964) и показывает теоретический фафик в логарифмическом масштабе по обеим осям для различных значений а.

На рисунке 14.5 приведен фафик в логарифмическом масштабе по обеим осям для ежедневных данных согласно индексу Доу-Джонса, используемых в данной книге. Область хвостов и для положительных, и для отрицательных хвостов имеет достаточно наблюдений для хорошего считывания а. Приблизительное значение в 1,66 соответствует более ранним исследованиям Фамэ (Fama, 1965b). -1

-2 -3 -4 -5

об -6 -о

-И -2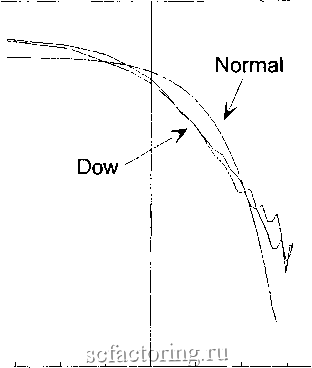

-15 -1 -0 5 О 0 5 1 Log(Pr(U>u))

РИСУНОК 14.5 Оценка альфы, графический метод: ежедневный индекс Доу-Джонса для

акций промышленных компаний.

Графический метод с логарифмическим масштабом по обеим осям работает хорошо в присутствии больших наборов данных, таких как ежедневные временные ряды индекса Доу-Джонса. Однако для меньших наборов данных он менее надежен.

Часть ф Фрактальный шум

Этот метод критиковал Кугаер (Cootner, 1964), который заявил, что одни толстые хвосты не являются неоспоримым доказательством того, что устойчивое распределение является единственным выбором. Эта критика еще более непреодолима в наши дни с появлением моделей ARCH и других распределений с толстыми хвостами. Следовательно, графический метод должен использоваться в сочетании с другими испытаниями.

R/S-анализ

Мандельброт не знал о методе нормированного размаха (18танализе) до конца 1960-х гг. Даже в то время его работа с использованием R/S-анализа бьша, прежде всего, ограничена его первоначальной областью исследований, гидрологией. Когда Фамэ писал свою диссертацию (Fama, 1965а), он также не знал о R/S-анализе. Однако он бьш знаком с рэнджевым анализом, как и большинство экономистов, и разработал взаимосвязь между масштабированием диапазона устойчивой переменной и а. В Главе 5 мы видели, что работа Феллера (Feller, 1951), прежде всего, имела дело с масштабированием диапазона и его отношением к показателю Херста. Здесь мы видоизменим работу Фамэ и приведем дополнительную информацию о нормированном размахе и показателе Херста.

Сумма устойчивых переменных с характеристическим показателем альфа приводит к новой переменной с характеристическим показателем альфа, хотя масштаб изменится. Фактически, масштаб распределения сумм равен п , умноженному на масштаб индивидуальных сумм, где п - число наблюдений. Если масштаб увеличивается с ежедневного до еженедельного, масштаб увеличивается на 5 , где 5 -число дней в неделю.

Если мы определяем сумму Rn как сумму устойчивой переменной в определенном интервале п, а Г как начальное значение, то имеет место следующее соотношение:

R = R,*n (14.8)

Это уравнение близко уравнению (4.7) для нормированного размаха. В нем показано, что сумма значений п изменяет масштаб п раз по сравнению с начальным значением. То есть сумма пятидневных прибьшей с характеристической альфой эквивалентна однодневным прибьшям, умноженным на 5 , Логарифмируя обе части уравнения (14,8) и вычисляя альфу, мы получаем:

а =-- (14.9)

log( )-Iog(R,)

Вспомним из уравнения (4,х), что log(w)

Если логарифм размаха Rr-Rri приблизительно равен нормированному размаху R/S, мы можем постулировать следующее соотношение: