

 |
 |
|
Факторинг Анализ финансовых западных рынков границы аттрактора, она возвращается к центру. Расходящиеся точки снова сблизятся, хотя для этого может понадобиться много орбит. Это явление - свойство чувствительной зависимости от начальных условий. Поскольку мы никогда не можем измерить текущие условия с бесконечным количеством точности, мы не можем предсказать, куда пойдет процесс в долгосрочной перспективе. Степень расхождения или потеря прогнозирующей способности может быть охарактеризована посредством измерения расхождения близлежащих орбит в фазовом пространстве. Степень расхождения (называемая показателем Ляпунова ) измерена для каждого измерения в фазовом пространстве. Одна положительная степень означает, что есть расходящиеся орбиты. Вместе с фрактальной размерностью это означает, что система является хаотической. Кроме того, должен быть отрицательный показатель для измерения процесса сворачивания или возвращения к атфактору. Формула для показателей Ляпунова такова: Lf lim [(l/t)*log2(p,(t)/pi(0))] (16,1) где Li = показатель Ляпунова для размерности i Pi(t) = положение в i-ой размерности, во времени t Уравнение (16,1) измеряет, как объем сферы растет со временем t посредством измерения расхождения двух точек, p(t) и р(0), в размерности i. Расстояние подобно многомерному диапазону. Исследуя уравнение (16,1), мы можем видеть некоторое сходство с R/S-анапизом и с вычислением фрактальной размерности. Все они связаны с масштабированием. Однако хаотические аттракторы имеют орбиты, которые убывают по экспоненте, а не в соответствии со степенными законами. ПРИМЕНЕНИЕ R/S-АНАЛИЗА Когда мы кратко изучали аттрактор Макки и Гласса (Маскеу and Glass, 1988) в Главе 6, мы бьши заинтересованы обнаружением циклов. В этой главе мы расширим это исследование и увидим, как R/S-анализ может различать шумовой хаос и дробный шум. Показатель шума В Главе 6 мы не раскрьши значение показателя Херста. Для Рисунка 6.8 Н=0,92. Как следовало бы ожидать, непрерывный, гладкий характер хаотического потока способствует очень высокому показателю Херста. Он не равен 1 из-за механизма сворачивания или инверсий, которые часто происходят в проекции прямой времени этого уравнения. На Рисунке 6.11 мы прибавили к системе одно стандартное отклонение белого, однородного шума. Это понизило показатель Херста до 0,72 и проиллюстрировало первое применение R/S-анализа к шумовому хаосу: использование показателя Херста как показателя шума. Предположим, что вы - технический аналитик, который хочет проверить определенный тип ежемесячного показателя момента, и для проверки показателя вы планируете использовать уравнение Макки-Гласса. Вы знаете, что показатель Херста для ежемесячных данных имеет значение 0,72. Чтобы сделать моделирование реалистическим, к данным необходимо добавить одно стандартное отклонение шума. Таким образом, вы можете увидеть, является ли ваш технический показатель устойчивым относительно шума. Теперь предположим, что вы - ученый, исследующий хаотическое поведение. У вас есть особый тест, который может отличить хаос от случайного поведения. Чтобы сделать этот тест практическим, вы должны показать, что он является устойчивым относительно шума. Поскольку большинство наблюдаемых временных рядов имеет значения Н близкие к 0,70 (как нашел Херст; см. Таблицу 5.1), вам понадобится достаточное количество шума, чтобы ваш испытательный ряд имел Н=0,70. Пли же вы можете постепенно добавлять шум и наблюдать уровень Н, на котором ваш тест становится недостоверным. 1.3 1.2 1.1 1 с 0-9 с 0.8 X 0.6 0.5 0.4 0.3 \ Н=0.72 ш---- Н=0.61 О 50 100 150 200 250 Observational Noise as а Percent of Sigma РИСУНОК 162 Уравнение Макки-Гласса, чувствительность показателя Херста к шуму. На Рисунке 16.2 показаны значения Н по мере добавления возрастающего шума к уравнению Макки-Гласса. Показатель Херста быстро понижается до 0,70, а затем постепенно падает до 0,60. Однако после добавления двух стандартных отклонений шума, Н все еще приблизительно составляет 0,60. Это означает, что частые значения Н=0,70, что так интриговало Херста OHurst, 1951), возможно, обусловлены тем фактом, что добавление шума к нелинейной динамической системе быстро заставляет значение Н упасть до 0,70. С другой стороны, данные Н ниже 0,65, которые обнаруживаются на рынках, вероятно, не вызваны просто добавлением измерительного или аддитивного шума к хаотическому аттрактору, но могут, вместо этого, быть вызваны дробным шумом. Эта возможность также подтверждает идею о том, что в краткосрочной перспективе рьшки представляют собой дробный шум, а в долгосрочной перспективе - шумовой хаос. Системный шум Помимо аддитивного шума, который мы исследовали, есть другой тип шума, называемый системным шумом . Системный шум имеет место, когда результат итеративной системы искажен шумом, но система не может отличить шумный сигнал от чистого и использует шумный сигнал как входные данные для следующей итерации. Этот вид шума весьма отличается от наблюдаемого шума, который происходит вследствие того, что у наблюдателя возникают трудности при измерении процесса. Процесс продолжается, не обращая внимания на нашу проблему. Однако что касается системного шума, шум вторгается в саму систему. Из-за чувствительной зависимости от начальных условий системный шум увеличивает проблему прогнозирования. На рьшках, вероятнее всего, представлять проблему будет системный шум, а не наблюдаемый шум. Представьте следующую ситуацию: для нас не составляет трудности узнать стоимость последней торговой сделки, но мы не знаем, была ли это справедливая цена или нет. Возможно, продавец был в отчаянии и должен был осуществить продажу по любой цене, чтобы соблюсти предписьшаемую маржу. Мы реагируем на этот шумный результат, не зная его истинное значение. Если задействован системный шум, то прогнозирование становится более трудным, и испытания должны быть скорректированы соответствующим образом. Воздействие системного шума на показатель Херста подобно воздействию аддитивного шума и показано на Рисунке 16.3. Н=0.70 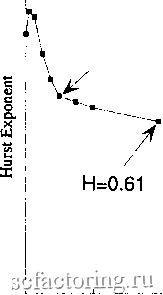 50 100 150 200 System Noise as а Percent of Sigma 0.6 РИСУНОК 163 Уравнение Макки-Гласса, чувствительность показателя Херста к шуму.
|