результаты были сопоставимы. Хаотические атфакторы, хотя они и получены опытным путем, кажутся подобными рыночным временным рядам в том, что они имеют неустойчивые дисперсии.

1 08 1 1 07 1 06 I 05 1 04 1 03 1 02 1 01 1

О 99 О 98

с .2

>

Q тз

и, ГЗ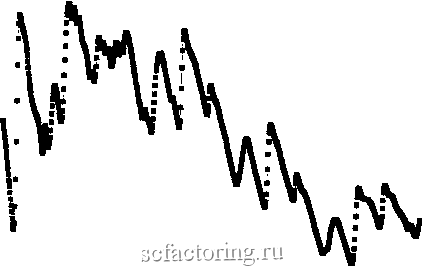

200 300 400 500 600 700 800

Number of Observations

0 97

900 1000 1100

РИСУНОК 175а Уравнение Макки-Гласса: последовательное стандартное отклонение.

1 OS

1 01

1-гз

-О (-

о 99

300 400 500 600 700 800

Number of Observations

1 ООО

и 98

РИСУНОК 175Ь Уравнение Макки-Гласса с наблюдаемым шумом: последовательное

стандартное отклонение.

.52 > о

Q Н

со с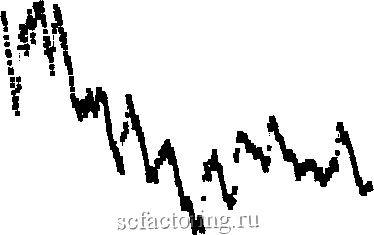

- I 035 1 03 I 1 025 1.0? 1 015 I 01 1 005 1

О У95 О 99

300 400 500 600 700 800

Number of Observations

О 985

1000 1100

РИСУНОК 175с Уравнение Макки-Гласса с системным шумом: последовательное

стаццартное отклонение.

Observational Noise

No Noise

0.05

-0.05

-0.1

200 300

-0.15

500 600 700 800 Number of Observations

900 1000 1100

РИСУНОК 17.6a Уравнение Макки-Гласса: последовательное среднее.

0.04

: 0.02

h /1

; , i;

л. 7

.300

500 600 700 800 Number of Observations

900 1000

-0.02

-0.04

i -0.06

- -0.08 1100

РИСУНОК 17.6b Уравнение Макки-Гласса с системным шумом: последовательное

среднее.

Подобно рыночным временным рядам хаотические аттракторы также имеют непостоянные средние значения; однако системы с шумом действительно напоминают рыночные временные ряды. Возможно, долгосрочные рьшочные временные ряды подобны хаотическим.

ИЗМЕРЕНИЕ а

Вторая характеристика ряда рынка капитала - показатель Херста между 0,50 и 1,00. Как следовало бы ожидать, чистый хаотический поток, подобно атфактору Лоренца или уравнению Макки-Гласса, будет иметь показатели Херста близкие к 1, но меньше 1, вследствие непериодического компонента цикла. Каково воздействие шума на показатель Херста системы?

Графический метод

Используя фафический метод из Главы 15, мы можем определить, что а приблизительно составляет 1,57 для системы с наблюдаемым шумом, как показано на Рисунке 17.7. Это дает приблизительное значение И = 0,64. Показаны и положительные, и отрицательные хвосты.