Умножая W на спереди, получим общее решение задачи минимизации дисперсии портфеля как функции Ё для акций 1, 2 и 3:

Акция 1 ai = -5.10753Р -f 0.787634. Акция 2 аз = -4.83871Р + 0.693548. Акция 3 аз = 9.946237Р-0.48118.

Например, если мы хотим получить ожидаем}ю доходность .1 (т. е. 10%), мы должны подставить .1 вместо Ё в приведенные выше формулы минимизирующих дисперсию весовых коэффициентов:

Акция 1 0.276882.

Акция 2 0.209677.

Акция 3 0.513441.

Сумма 1.000000.

2.6 Вид границы

Если мы найдем решение задачи минимизации риска в большом диапазоне ожидаемых доходностей, то увидим, что граница имеет форму нули . Интуитивное понимание, почему граница имеет именно такую форму, можно получить, рассмотрев случай двух типов акций. Предположим, имеются два вида акций с ожидаемой доходностью E{ri) и Е{г2), стандартными отклонениями <Ti и ог и ковариацией o-jj. Если мы рассмотрим комбинацию из а акций первого типа и (1 - а) второго, ожидаемая доходность портфеля aE(ri) + (1 - а)Е{г2) будет находиться где-то между E{ri) и Е{г2). Стандартное отклонение портфеля равно

[aV?-f (1 - а)Ч+ 2а(1 - a)<7i/. 55

Для того чтобы граница имела выпуклую форму, требуется, чтобы стандартное отклонение портфеля было меньше линейной комбипации acri + (1 - а)<Т2 при О < а < 1 и больше - при а < О или а > 1. Другими словами, мы должны проанализировать неравенство

[a<7l + {l-aY(Tl + 2a{l-a)<7,2f < аа, + {1 - а)<72. Возводя обе части в квадрат и упрощая, получим

а(1 - a)<Ti2 < а(1 - a)<Ti<T2.

Величина = cri2/cri(T2 называется коэффициентом корреляции (correlation coefficient). В теории вероятностей доказываются неравенства -I < Pi2 < I Для любых случайных величин. При-1 < Pi2 < 1 мы получаем требуемое неравенство:

q(1 - q)<Ti2 < а(1 - a)(Ti(T2, если О < а < 1, или

а(1 - a)<Ti2 > а(1 - a)<Ti<T2,

если а < О или а > 1. Если же pi2 = 1 или pi2 = -1, то граница может быть кусочно-линейной. Мы, однако, не будем всерьез рассматривать этот вырожденный случай.

2.7 добавление

безрисковых активов

Предположим теперь, что имеется безрисковый актив с доходностью Гу. Это соответствует точке на оси F, поскольку безрисковый актив, но определению, имеет нулевую дисперсию.

Наличие безрисковых активов меняет открытые перед на-ЛИ инвестиционные возможности, поскольку мы можем комбинировать его с рисковыми активами. Фактически меняется эффективная граница инвестиционных возможностей. Проиллюстрируем это положение, используя следующий рисунок: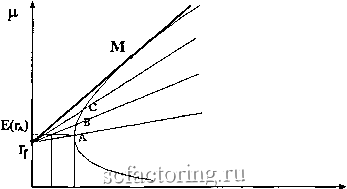

Рассмотрим точку типа Л, которая соответствует портфелю с ожидаемой доходностью Р(гд) и стандартным отклонением (Тл- По мы можем получить ту же самую ожидаемую доходность, но с меньшей дисперсией, составив комбинацию портфеля точки В с безрисковым активом. Если мы инвестируем авгу к (1 - а) в В, то ожидаемая дохощгасть будет arj -f (1 - а)Е(гв), а стандартное отклонение (1 - а)ав- Выбрав а подходящим образом, как показано на рисунке, мы получим ту же самую ожидаемую доходность с меньшим риском.

Продолжая в том же духе (рассмотрев, например, точку С), мы обнаружим, что самое лучшее, что мы можем сделать, это составить комбинацию из безрискового актива и точки М На рисунке. Это приводит к следующей эффективной границе: