Аналогично, если нредноложить, что Р - С + S < X, мы можем получить гарантированную прибыль, купив акцию, купив пут-онцион и продав колл-опцион. Таким образом, гарантированная прибыль невозможна только тогда, когда Р - С + S = X, что и нредставляет собой взаимосвязь нут-колл .

Если г = 1 + безрисковый процент > 1, то взаимосвязь нут-колл для европейских опционов имеет вид

S+P-C = Х/г.

Это означает, что портфель, состоящий из акции, пут-опциона и короткой нозиции но (проданному) колл-опциону, будет продаваться и покупаться по цене, равной текущей цене исполнения, дисконтированной на безрисковый процент.

3.6 Несколько периодов:

европейский колл-опцион

Когда цена акции может принимать лищь одно из двух возможных значений, ноток платежей от колл-опциона можно воспроизвести при помощи портфеля, состоящего из акций и безрисковых активов. Когда число возможных значений цены больще двух, непосредственное воспроизведение, вообще говоря, невозможно. Однако можно рассмотреть процесс изменения цен, состоящий из нескольких периодов, где в каждом периоде используется уже рассмотренная биномиальная модель. Полагая число периодов достаточно большим, а длину периода достаточно малой, можно получить много возможных состояний (возможных значений цены) на финише. В пределе этого процесса получается модель Блэка-Шоулза для цен на опционы.

Общая формулировка двухнериодной задачи такова.

5 = текущая цепа акции,

С = чека на колл-опциоп, подлежащая определению. Предположим, что в конце первого периода цена может принимать два значения:

Su - высокая цеиа акции в конце периода 1

(состояние II), Sd - низкая цена акции в конце периода 1 (состояние L). Предположим, что в конце второго периода для каждого из состояний {II и L) снова возможны два значения цепы:

Suu = высокая цепа акции в конце периода 2

при высокой цене акции в конце периода 1; Sud - низкая цена акции в конце периода 2

при высокой цене акции в конце периода J; Sdu = высокая цена акции в конце периода 2

при низкой цене акции в конце периода J; Sud = низкая цена акции в конце периода 2

при низкой цене акции в конце периода 1. Возможные траектории цен представлены на следующей диаграмме:

Цена акции Suu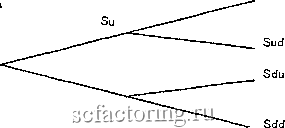

Период 1 I Период 2 ~ Время

Обозначим X = цена исполнения,

г = 1 + безрисковый процент на активы

за один период

(одинаков для обоих периодов).

Терминальные значения для колл-опционов таковы:

Сии = тях{0, Suu - Х],

Cud = max{0, Sud - X},

Cdu = max{0,5du - A},

Cdd = ma.x{Q,Sdd-X),

где предполагается, что Suu > Л (в противном случае онцион никогда не исполняется и цена его равна нулю).

В начале периода 2 мы знаем, как найти цену опциона на этот период, так как эту задачу мы уже решали. Пусть Си - цепа колл-опциона, & ки - коэффициент полного хеджирования при условии, что в периоде 1 цена выросла (реализовалось состояние II):

Си - Su/ku - (Suu - киСии)1киГ, где ки = (Suu - Sud)l(Cuu - Cud)-Аналогично выражается Cd

По тогда через Си и Cd можно выразить значение С - цену колл-опциопа в начале периода 1:

С = S/k-(Su- кСи)/кг, где к= (Su- Sd)/(Cu-Cd).

Разница между этими формулами и аналогичными формулами для задачи на один период состоит в том, что Си и Cd