то трейдер типа 21 должен купить столько портфелей, сколько возможно, поскольку он получит доход при покупке, а потери в конце периода будут равны пулю. Аналогично, если 5 - ЗС > О, то трейдер 71 должен продавать сколько возможно.

Трейдер Т2 знает, что колл-опцион ничего не принесет (поскольку цепа иснолнения равна 30), так что полумаем С = 0. Вместе эти два ограничения дают 5 = О, С = 0. Чтобы определить цену пут-опциона, исхюльзуем взаимосвязь iiyT-колл (эго соотношение обсуждалось в раздсгге, посвя-тценпом опционам): 5 -j- 7 - С = 30, отк}ла получаем Р = 30.

Заметим, что требование отсутствия арбитража реалыю накладывает огразгичения па цепы покупки и продажи (бидь: и аски), поскольку единственный способ получить арбитраж-]1ЫЙ выигрыш - это принять имеющийся бид или аск. Таким образом, отсутствие арбитража подразумевает, что

1. 5 -ЗС > О, так что трейдер Т1 не может купить такой портфель но отрицательной цене,

2. 5 - ЗС < О, так что трейдер 71 не хюжст продать такой портфель по положительной цене,

3. С < О, так что трейдер Т2 не кюжет продать колл-опцио]! но положительной цепе,

4. С > О, так что трейдер Т2 не может купить колл-опцион но отрицательной цене.

Поскольку биды и аски должны быть неотрицательны, условие 3 сводится к С = О, а условие 4 является itecyme-ствепным.

В этом примере мы обратились к двум портфелям: 5 - ЗС = 0иС = 0, ]газываемым сепарирующими , поскольку они разделяют информацию двух типов трейдеров. Оказывается, что для каждого из трех состояний отсутствие арбитража влечет рациональные ожидания. Сепарирующие портфели для двух типов трейдеров приведены в таблицах:

Состояние

С]1язь между арбитражем и эф()ектив1Юстыо jjciko видтга па графике. Например, если истиппос состояние z, ии можем нарисовать графики уравнений сепарирующих порт4*слсй: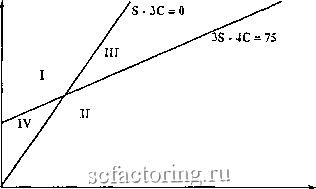

Па этом рисунке трейдер типа Т1 захочет купить любой такой портфель, что 5 -ЗС < О, и продать, если j-SC > 0. Л][алогичпое утверждение относится к трейдера типаГ2. Это означает, что мы не будем наблюдать какие-либо комбинации

бидов па акдию/асков па колл-оппиоя в области, помсчсппой Т, и ПС будем наблюдать комбинации асков на акцию/бидов па колл-опцион в области, помечезгной ТГ. Б областях 111 и IV трейдеры одтюго типа захотят осуществить покупку, а другого - продажу. OiUiaKO поскольку желаемые сооткопгс-ния между акциями и колл-опционами различны д.тгя разных групп, такая ситуация не может сохраняться.

Особезшо простой случай сепарировазшя возникает для со-стоя]1ия у. Здесь для агрегирования информации доста гочтго границ на цепы акций, поско.льку трейдерам Tmia 71 изнсст-но, что 5 > 25, а трейдерам типа 7 2 - что S < 25. Таким образом, мипималыю возкюжная сТоиьюсть для типа 7 2 является максималыю возможной для типа 71. В общем случае, если портфель является сенарирующиг, то о][ может бьггь охарактеризован в терминах минимального и максимального платежей. ТГусть min, обозначает минимальный платеж по тюргфелю при имею1цсйся у трейдера i ип(})ормации, а шах, обозначает соотпетстпующий максимальный платеж. Тогда ]1ортфель сепарирует в том и только в том случае, когда

max {min,} - min {niax,} i i

Эти рассуждения не будут иметь места, если количество опцио]юв псдостаточлго. В предельном случае, если онцио]гов пет вовсе, требовазгие отсутствия арбитража почти не ограничивает це]1Ы.

4.7 Рациональные ожидания с помехами

Цель дан]юй теории - попытаться навести мост между наблюдаемыми явлениями и предсказа]1иями теории рационсьть-иых ожиданий. Рассматривается рынок ценных бумаг, на котором трейдеры формируют рациональные ожидания, однако