

 |
 |
|
Факторинг Теория Эллиотта применима к прямоугольным треугольникам, где сумма квадратов двух более коротких сторон равна квадрату самой длинной сторо- 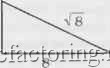 ны. Справа приведен пример, использующий Fg, Fg и квадратный корень из F . 9. Формула, показывающая отношение между двумя наиболее распространенными иррациональными числами в математике, тг и ф, приведена ниже: F= 100 X тгх ф 1, где ф= 0,618..., п представляет собой порядковый номер в последовательности и F представляет сам по себе член последовательности. В данном случае число 1 представлено только одшт раз, так что F, = 1. F = 2, F3 = 3, = 5 и так дачее. Например, пусть п = 7. Тогда Fy =100x3,14162x0.6180339 =- = = 986,97x6180336 = = 986,97x0,021129 = 21,01 10. Одно из удивительных явлешш. которое, насколько нам известно, до сих пор не упокшналось, состоит в том, что отношения между числами Фибоначчи равны числам, очень близким к тысячным долям др>тих чисел Фибоначчи, при разности, равной тысячной доле еще одного числа Фибоначчи (см. рис. 3-2). Ткк, в направлении возрастания отнощение двух идентичных чисел Фибоначчи равно 1, или 0,987 плюс 0,013: соседние числа Фибоначчи имеют отношение 1.618. или 1,597 плюс 0,021; числа Фибоначчи, расположенные с двух сторон от некоторого члена последовательности, имеют отношение 2,618, или 2,584 плюс 0,034, и так далее. В обратном направлении соседние числа Фибоначчи имеют отношение 0,618. или 0,610 плюс 0,008; числа Фибоначчи, расположе1Шые с двух сторон от некоторого члена последовательности, имеют отношение 0,382, шш 0,377 плюс 0,005; числа Фибоначчи, между кото- пыми расположены два члена последовательности, имеют отношение 0.236, или 0,233 плюс 0,003; числа Фибоначчи, между которы-tи располоэкены три 4J№Ha последовательности, имеют отношение О 146. или 0.144 плюс 0,002; числа Фибоначчи, между которыми расположены четыре члена последовате-чьности, имеют отношение О 090. или 0,089 плюс 0.001; числа Фибоначчи, между которыми расположены пять членов последовательности, имеют отношение 0,056. или 0,055 плюс 0,001; числа Фибоначчи, между которыми расположено от шести до двенадцати членов последовательности, имеют отношения, которые салга являются тысячньгми долями чисел Фибоначчи, начиная с 0,034. Интересно, что в этом анализе ко-эффищепт, связывающий числа Фибоначчи, между которылш располагаются тринадцать членов последовательности, снова начшта-ет ряд с числа 0,001, с тысячной доли того чиста, где он начался! При всех подсчетах мы действительно получаем подобие или самовоспроизведение в бесконечном ряду . раскрывающее свойства самой прочной связи среди всех NiaTeMaTH4ecKHx отношений . И, наконец, заметим, что (V5 + 1)/2 = 1.618 и [\- 1)/2 = 0.618. где \5 = 2,236. 5 оказывается наиболее важным для волнового принципа числом, а его квадратньш корень является математическим ключом к числу ф. Число 1,618 (или 0,618) известно как золотое отношение, или золотое среднее. Связанная с нш.1 пропорциональность приятна для глаза и уха. Оно проявляется и в биологии, и в музыке, и в живописи, и в архитектуре. В своей статье, вышедшей в декабре 1975 года в жу-рнале Smithsonian Magazine, Вильям Хоффер сказал: ...Отношение числа0,618034к 1 являетсл математической основой формы игральных карт и Парфенона, подсолнуха и морской раковш1ы. греческих ваз и спиральных галактик BHCujnero космоса. В основании очень многих произведений иС1сусства и архитектуры греков лежит эта пропорция. Они называли ее золотая середина . Плодовитые кролики Фибоначчи выскакивают в самых неожиданных местах. Числа Фибоначчи, несомненно, являются частью JvmcTH4ecKoft природной гармонии, которая приятна для ошуще-1ШЙ, приятно выглядит и даже звучит приятно. Музыка, к гфиме-РУ. основана на октаве в восемь нот. На фортепиано это представлено 8 белыми и 5 черными клавишалга - в целом 13. Не случай- но. что музыкальный интервал. принося1Ц11и нашему слуху самое большое наслаждешге - это секста. Нота лш вибрирует в отношении 0.62500 к ноте до . Это всего лишь на 0,006966 отстоит от точной золотой середины. Пропорции сексты передают приятные для сл\тса вибрации улгггке среднего уха - органа, который тоже имеет форму логарифмической спирали. Постоянное возшткновение чисел Фибоначчи и золотой спирали в природе точно объясняет, почему отношение 0,618034 к 1 настолько приятно в произведениях искусства. Человек видит в искусстве отражешге жизни, которая имеет в основании золотую середину . Природа использует золотое отношение в своих наиболее совершенных творега1ЯХ - от таких мелких, как микроизвилины мозга н молекулы ДНК (см. рис. 3 9), до таких крутгаых, как галактики. Оно проявляется в таких различных явлениях, как рост кристаллов, пре-лом.леш1е светового луча в стекле, строение мозга и нервной системы, музыкальные построештя, структура растений и животных. Наука предоставляет все больше свидетельств того, что у природы действительно есть главпьш пропорциопалыгьш принщш. Кстати, вы держите эту книгу двумя из своих пяти пальцев, причем каждый палец состоит из трех частей. Итого; пять единиц, каждая из которых делится на три - прогрессия .5-.3-.5-3, подобная той, что лежит в основе волнового принципа Золотое сечение Любой отрезок может быть поделен таким образом, что отиошс ние его медшшей части к большей окажется таким же. как и отношение большей части ко всему отрезку (см. рис. 3-3]. Это отношение равно 0.618. Золотое сечение встречается в природе повсеместно. Человеческое тело соответствует приншту золотого сечения (см. рис. 3-9) фактически во всем, начиная от внешних размеров и заканшвая чертишь .лица. Платон в своем Игмее пошел так далеко, - говорит Питер Томпкгшс. - что рассмотрел число ф и вывел пропорщш золотого се чения - всеобъемлюхцее математическое соотношение и увидел в нем ключ ко всей природе космоса . В XVI столетии Иоганн Кеплер, говоря о золотом, или божественном , сечешш, наго1сал. что фактичес  Рис. 3-3 ки оно от1сьшает все создашюе и символизирует Божественное тво-pemie по своему подобию . Путюк делит человеческое тело по гфин-щщу золотого сечеш1я. Для статисгического усреднешш используется число, примерно равное 0.618. Отношеш1е остается верным отдельно для мужчин и отдельно для женщин, что есть символ творения по своему подобию*. Является ли и прогресс человечества творением по своему подобию ? Золотой прямоугольник Стороны золотого прямоутольника имеют отношение 1.618 к 1. Чтобы построить золотой прямоугольник, начните с квадрата со сторонами, равными двум единицам, потом проведите линию от середины одной стороны квадрата к одтюй из его вершин, образуто-шпх противоположную сторону как показано на рис. 3-4.  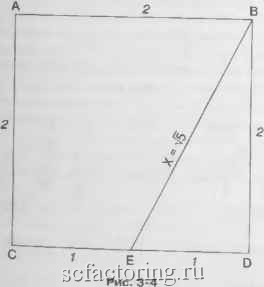 Треугольник EDB является прямоугольным. Около 550 года до р.х. Пифагор доказал, что квадрат гипотенузы (X) прямоутольиого треугольника равен сумме квадратов двух других его сторон. В данном случае Х= = 2 + 1=. или Х = 5. Длина стороны ЕВ, таким образом, должна быть квадратным корнем из 5. Строя золотой прялюуголь-ник, следующим шагом продлите отрезок CD и постройте на нем отрезок EG, равный квадратному корню из 5, или 2,236 единищ,! длины, как показано на рис. 3-5. В построенных таким образом пря-моутольниках стороны связаны золотым коэффициентом. Таким образом, и прямоугольник AFGC, и прямоугольник BFGD являются золотыми. Доказательство этого факта следующее: 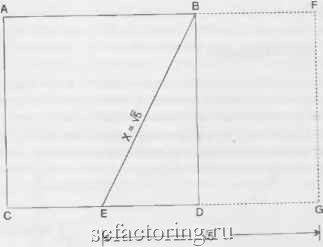 Рис. 3-5 CG = V5+ 1 FG = 2 CG n5 + 1 FG 2 2.236 + 1 2 3.236 2 = 1.618 DG = 5-1 FG = 2 DGVS FG 2 2.236-1 . 2 1.236 2 = 0.618. Поскольку стороны прямоугольников связаны золотым отношением, следовательно, эти прямоуго.льники, по определештго, являются золотыми прялюугольниками. Использование золотого прямоугольника в произведениях ис-кчсства чрезвычайно усиливает их привлекательность. Особенно сильно были очарованы золотым прямоугольником древтше египтяне и греки, использовавшие его весьма часто. Не забывали о нем и художники Ренессанса, как, впрочем, и всех других наивысших моментов развития цивилизации. Большое значение зо-лотомл отношению придавал и Леонардо да Винчи. Он находил красивыми задаваемые им пропорщи и говорил, что если вещь выглядит неправильно, она не работает . Многие из его 1сартин выгляде;п1 прекрасно, потому что он сознательно использовал золотой прямоугольник для усиления их привлекательности. Античные и современные архитекторы, и в особенности строители Парфенона в Афинах, неизменно придерживались правила золотого прямоугольника. Очевидно, на 1еловека, созерцающего форму, пропорции, связанные с числом ф, оказывают воздействие. Исследователи обна-ружи-ли, что люди находят такие формы эстетически привлекательными. Например, при проведении эксперимента людей просили выбрать из группы различных прямоугольников один. В общем случае выбор склонялся к прямоугольникам, форма которых была близка к золотому. Когда испытуемых проси.ли произвольно разделить отрезок, они были склонны делить его в отношении ф. Окна, картинные рамы, здания, книги и кладбищенские кресты часто являются приближениями к золотомл прямоугольнику. Как и в случае золотого сечения, значение зо.лотого прямоугольника не исчерпывается его красотой, но, по-видимому, обсл>Ж1тва-ет и функциональные задачи. Среди множества примеров наиболее уд1шите.тьный состоит в том, что двойная спираль ДНК сама создает точтшхе золотые прямоугольники, изгибаясь с правильными интерваталш (см. рис. 3-9]. В то время как золотое сечение и золотой прямоутольпик предоставляют собой статистые формы природной или рукотворной кра-оты и функциона.льности, наиболее ярким представ-лепием эстетически приялтюго динамизма, упорядоченного роста или прогрес-
|