дером двух или большего числа независимых оснований (признаков, индикаторов) для принятия решения об открытии торговой позиции. Иными словами, исходя из данной аналогии можно сделать общий вывод: чем больше независимых признаков использует трейдер, тем более вероятен успех, т.е. какой-то из признаков да сработает.

Таким образом, если ставка делается на молодость тренда, то необходимы дополнительные индикаторы, которые могли бы подтверждать силу этого тренда, скажем, по более глубокой истории или каким-то техническим соображениям. А при ставке на старый тренд, который статистически уже проверен, обязательно потребуются признаки, свидетельствующие об отсутствии истощения .

Разумеется, возможны и иные подходы. Здесь же, поскольку мы говорим о вероятностном анализе, интересен другой вопрос: могут ли возникать тренды в случайных процессах? Ведь здравый смысл настойчиво подсказывает, что естественнее всего был бы равномерный беспорядок.

Вот когда читателю представился случай убедиться в том, что наш внутренний голос не всегда бывает прав.

9.3.3. О законах (теоремах) арксинуса

Законы арксинуса (известные также как первая и вторая теоремы), в частности, показывают, что в случайных процессах тренды возникают почти неизбежно. Мы не будем утомлять читателя математикой строгих выкладок. Но если кому-то хочется узнать об этой интересной особенности жизни случайных чисел, с тем чтобы применить ее на практике, то ниже будет дана общая формулировка первого закона, кратко изложенного в прикладной форме.

Обратимся опять к монете. Но не как к дорогому сердцу всякого трейдера денежному знаку, а в качестве генератора случайных чисел. Вновь займемся бросками на удачу и результат каждого испытания будем обозначать точкой в двухмерном пространстве:

ПО вертикали. Шаг вверх, если выпадает какая-то заранее обозначенная сторона (прибыль); если другая - шаг вниз (убыток);

по горизонтали. Каждый номер броска - это один шаг вправо (очередное вхождение в рынок).

В результате множества бросков получим набор точек, соединив которые, увидим некоторую линию, берущую начало из координаты (О, 0), а далее уходящую в неизвестность. Такой путь в теории вероятности называют кривой случайного блуждания . Очевидно, что она весьма близко отражает игровую ситуацию трейдер против рынка . Игрок тоже блуждает по этому минному полю, то выигрывая (допустим, верхняя половина пространства), то теряя (нижняя). Поэтому задачи, теоретически решаемые в связи с этой моделью, могут иметь для нас известное практическое значение.

Вопрос формулируется просто: если рынок считать явлением случайным и поэтому решение об открытии позиции принимать на основе серии последовательных бросков монеты угадал - не угадал , то какова вероятность оказаться в выигрыше (в данном случае - в верхней части пространства блуждания) по суммарным результатам какого-то определенного числа испытаний?

Здравый смысл подсказывает, что раз процесс случайный, то и распределение точек по обе стороны разделительной полосы должно быть приблизительно равномерным. Но эта подсказка никуда не годится. Потому что одно из самых неожиданных свойств чистой случайности заключается в том, что равномерное распределение после каждой отдельной серии испытаний встречается крайне редко.

Собственно говоря, в этой истине и состоит первый закон арксинуса. Он разрушает наши интуитивные представления о том, что при бросках идеальной монеты выигрыш примерно должен быть равен проигрышу. И дело в том, что это не просто неверно, а совершенно неверно. Иными словами, подсказка здравого смысла и реальная действительность сто-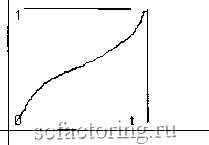

Рисунок 14.

График функции Р = f(t)

Хотя формула выведена для условия бесконечного числа бросков, но приличное ее приближение фактически обеспечивается начиная уже с 20 испытаний.

Из этого закона следуют два важных вывода.

Во-первых: вероятность для трейдера провести большую часть времени на выигрышной стороне гораздо ближе к О или 1, чем к интуитивно ожидаемому значению 1:2.

Во-вторых: чем больше число испытаний, тем более очевидным будет волновой характер случайного блуждания, при котором все точки будут группироваться примерно по синусоиде (не отсюда ли правило перемен Эллиотта?).

ят друг от друга, как мы увидим, на весьма неблизком расстоянии.

Если говорить более конкретно, то согласно первому закону арксинуса при фиксированном t (0<t<1) вероятность (Р) того, что доля времени (к/п), проведенная точкой в верхней половине, т.е. доля выигрышных для трейдера бросков (к), при их общем числе (п), стремящемся к бесконечности, будет меньше t, определяется по формуле:

Р = (2/3,14) xarcsin(tV2.

Графически функция Р = f(t) представляет собой кривую такого вида (см. рис. 14):