

 |
 |
|
Факторинг Теория очередей и материальные запасы можно ожидать, что если два распределения имеют некоторое число одинаковых моментов, то они в какой-то степени схожи и аппроксимируют друг друга. Обоснованием этого суждения является совпадение их аппроксимаций по методу наименьших квадратов при конечном размахе и разложений по ортогональным многочленам - при бесконечном ...Практически аппроксимация такого рода оказывается очень хорошей, даже если совпадают только первые три или четыре момента . В той же книге приводятся необходимые и достаточные условия возможности построения по моментам характеристической функции, однозначно определяющей распределение во всех точках его непрерывности. Эти условия, как правило, выполняются, хотя известны и отрицательные примеры (логарифмически нормальное распределение). При всех своих недостатках (чаще потенциальных, чем реальных) метод моментов остается наиболее удобным в работе и обычно применяемым методом выравнивания распределений. Количество сохраняемых моментов рассматривается как порядок аппроксимации. Оно равно числу свободных параметров теоретической кривой. Отметим также, что наращивание числа учитываемых моментов не всегда сопровождается монотонным улучшением качества аппроксимации; любое число учтенных моментов не может обеспечить хорошего согласия на хвосте распределения - в области малых значений ДФР (по опыту расчетов - менее 0.01); относительная погрешность высших моментов, найденных статистическими методами, быстро возрастает по мере увеличения порядка моментов. Поэтому практически ограничиваются выравниванием не менее двух (см. разд. 9.2), но не более четырех моментов. Существуют методы, позволяющие автоматически выбрать тип выравнивающего распределения в заданном семействе (например, одну из кривых К. Пирсона выбирают по четырем моментам - см. [56]). Критерии согласия ( Р. Фишера, па; Н.В. Смирнова, А.Н. Колмогорова) статистических и теоретических распределений с несколькими общими моментами мало чувствительны к виду распределений. Это позволяет в классе функций с заданными несколькими моментами выбирать дающие те или иные вычислительные преимущества - например, допускающие 3.3. Типовые распределения 69 эффективное вычисление ДФР или облегчающие расчет функционалов специального вида. Именно такие распределения (в первую очередь показательное и родственные ему) и будут использоваться в дальнейшем. При выборе типа аппроксимации важно знать степень отличия исходного распределения от показательного при равенстве средних значений. В первом приближении мерой отличия может служить коэффициент вариации (для показательного закона г; = 1 ). Однако с целью единообразного представления отличий в высших моментах удобно ввести набор коэффициентов немарковости ii = !ilf\-i\, г = 2,3,... (3.2.1) С помощью (3.1.5) легко проверить, что для показательного распределения все они равны нулю. З.З. Типовые распределения 3.3.1. Распределения фазового типа Пусть процесс проходит систему фаз с показательно распределенной задержкой в каждой из них. Распределение Эрланга г-го порядка имеет плотность дополнительную функцию распределения (ОЕ (3.3.2) И моменты Д = г(г + 1)... (г -Ь - 1) , - = 1,2,... (3.3.3) Оно предполагает последовательное прохождение г фаз (см. рис. 3.1). >°Д/7\-УЛ---- выход 1 2 г Рис. 3.1. Эрланговское распределение Дисперсия эрланговского распределения D - vjp? . Распределение Эрланга - двухпараметрическое, причем г должно быть целым. Это обстоятельство определяет следующую схему подбора параметров распределения Эрланга: 1) найти т - \j\jD -\- 0.5] (ближайшее целое к указанному отношению); 2) вычислить вещественный параметр = vjji . При этом строго выравнивается первый момент и приближенно - второй. Гиперэкспоненциальное распределение. Представление ДФР в виде F(0 = 2/.e- (3.3.4) позволяет считать исходный процесс проходящим одну из п альтернативных фаз. Здесь {уг\, О < < 1, Yi-\ Уг - 1 интерпретируются как вероятности выбора г-й фазы, а {fii} - как параметры показательного распределения времени пребывания в ней. Диаграмма гиперэкспоненциального распределения приведена на рис. 3.2. ВХОД 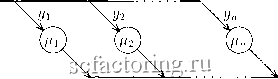 ВЫХОД Рис. 3.2. Гиперэкспоненциальное распределение Среди названных величин могут быть комплексные (попарно сопряженные), что подчеркивает фиктивный характер расщепления процесса на фазы. Допустимость таких параметров была впервые отмечена Д. Коксом в 1955 г. Использование формулы для моментов показательного распределения приводит к системе уравнений относительно параметров аппрок-
|