1) Вычислить дп = y/2Xg/{f bn) . Если qn > Уп-i . qn оптимально.

2) Если qn < Уп-1 , рассчитать g-i

3) Если qn-i > Уп-2 сравнить L(qn-\) с L{yn-i) , и минимум из них даст оптимальное q .

4) Если qn-i < Уп-2 , вычислить qn-2

5) Если qn-2 > Уп-з , минимум из L(qn-2) , и Ь{Уп-2) даст оптимальное q , и т.д.

Процедура требует не более чем п шагов.

Во втором случае дается дифференциальная скидка на каждую дополнительную единицу, приобретаемую сверх очередного порога. Здесь оплата хранения пороговой партии может быть отнесена к фиксированной составляющей стоимости заказа, и формула Уилсона дает оптимальное приращение относительно этого порога. Итоговая функция затрат имеет вид нижней огибающей семейства кривых, а глобальный минимум совпадает с наименьшим из минимумов образующих кривых. Примеры соответствующих графиков показаны на рис. 5.3.

В общем случае все параметры модели могут зависеть от объема партии. Пусть цена закупки есть b(q) , цена хранения h = f - b(q) . Стоимость восполнения д = д qb[q) . Целевая функция

Здесь / - цена хранения (в долях цены) \л д - стоимость заказа, не зависящая от объема партии. Интенсивность спроса Л считается постоянной, заказ выдается при снижении запаса до нуля. Функция затрат получается разрывной комбинацией кривых L(q) , и оптимальное решение достигается в минимуме одной из них [д , рис. 5.2а) или в точке разрыва [д , рис. 5.26).

Алгоритм оптимизации: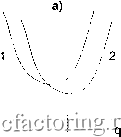

q q q q

Рис. 5.2. Минимальные затраты при интегральной скидке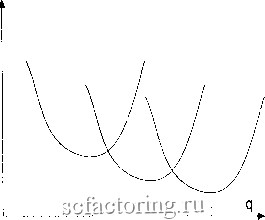

Рис. 5.3. Минимальные затраты при дифференциальной скидке Решение зависит от вида h[q) . В случае b{q) - ho-biq, bo bi ,

fbo-2Xbi

и находится методом итераций.

Практический интерес вызывает задача определения продажной цены изделия v с учетом зависимости от нее интенсивности спроса л .

R = cX-

hS 9 +

Будем считать, что интенсивность спроса определяется относительной удовлетворенностью потребителей -s/{S - s) согласно

д Ло \o(S -s)

S-(a + l)s

где a - постоянный множитель. С учетом этой зависимости

д сЛо(5 - s) - Ход

S-{a + l)s 2{S-s) Дифференцирование R(s, S) дает условия оптимальности

сАо cXo(S-s)-Xog S q

S-{a+l)s (5-(a + l)s)2 S-s2\S cXo , {a + l){cXo{S - s) - Ход) hf S

S-ia + l)s (5-(a+l)s)2 2\S-s

= 0.

С помощью математического пакета Maple V удалось установить, что оптимальный верхний порог S* является корнем кубичного уравнения

cahz - (а + l)ghz - 2Хд = 0.

Будем считать, что спрос обеспечивается полностью, а себестоимость единицы продукции составляет и . Используя для затрат на снабжение формулу Уилсона (5.1.10), можно для дохода в единицу времени записать выражение

R={v-u)X{v)-y/2gh\{v). Максимальный доход достигается при dR/dv = О , или при

V = и -

Это уравнение решается методом итераций.

Рассмотрим конкретизацию данного подхода. В модели с дефицитом и мгновенными поставками доход за цикл

RT = cXTg--, длина цикла Т = {S - s)/X . Соответственно доход в единицу времени