Начальное приближение для 5* выберем из условия компенсации потерь CS от неудовлетворенного спроса за цикл экономией на организации поставок. Максимизируя сумму gS/[S - 5) -f c.s , получаем

5 = 5- \fgSjc.

5.2- Хранение продукта

при естественной убыли

Предположим, что спрос на предмет хранения имеет постоянную интенсивность л , скорость восполнения составляет р , а скорость естественной убыли в каждый данный момент пропорциональна (с коэффициентом 7) наличному запасу. Динамика изменения запаса за один полный цикл длительности Т показана на рис. 5.4.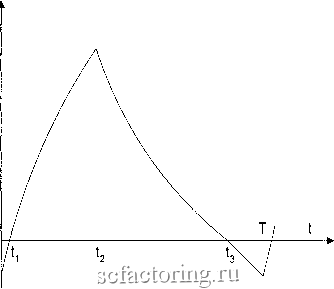

Рис. 5.4. Динамика запаса при естественной убыли

и описывается дифференциальными уравнениями

{ -А, 0</<<1,

/t-A-72/, h<t<h,

-А - 72/, t2<t< t3,

-А, t3<t<T

с решениями

y{t) =

l-A(i-<3),

<2 </ <<3.

h<t<T.

Из условий 1/(0) = s (уровень начала восполнения) и j/(b) = 5 (максимальный запас) определяем постоянные интегрирования. Окончательно

s-\-{n-X)t, 0<t<ti,

l e-7(->)](/i A)/, t<t<U,

(5 + A/7)e-T(--)-A/7, t.KtKh,

[-Xit-ts), t3<t<T.

Вычислим затраты Lt за цикл. Очевидно, затраты на хранение

г (Л)

2/(0

(5.2.1)

а сумма штрафов

j y{t) dt + J y(t) dt

.0 t3

Потери от убыли можно определить по разности между поставленным за цикл количеством продукта и его фактическим потреблением, так что

=c(/it2-AT).

Добавим к этим затратам расходы на организацию цикла д и перейдем к затратам в единицу времени. Исключая слагаемое -сХТ/Т = -сХ как

не зависящее от выбора управляющих параметров, приходим к

ь ti т

L\ghJ y[i) di-d

j y(t)dt + j y{t)dt

0 t3

+ cpt2} T. (5.2.2)

Вычислим входящие в это выражение интегралы. Из условий y(/i) О , у(Ь) = S , у{1з) - О , у{Т) - S можно получить временные параметры

h = <2+iln(l + ), Т = <3 + s/A.

(5.2.3)

Разобьем интеграл в (5.2.1) на две части и найдем их величину. Первая часть

dt =

JJ. - X

7 <--=(-Н

t2-ti

7 L 7

--In

fl - X J fl - X

Аналогично

Jy(t)dt = i[5-Al (l4-f)

Наконец, из элементарных соображений

ti т

y{t) dt = -

2( -Л)

о 1з

Из (5.2.3) можно получить явное выражение длины цикла

Подстановка полученных выражений в (5.2.2) дает искомую функцию затрат.