постоянства группировок. Очевидно, что минимум функции Ь{Т) , задаваемой правой частью (6.2.4), равен наименьшему из минимумов ее, достигаемых при постоянной группировке номенклатур. Наивыгоднейший период при постоянной группировке определяется приравниванием нулю производной dL/dT:

\ г=:1 * г=1

Ему соответствуют минимальные затраты в единицу времени

L* =

(6.2.7)

Обозначим числитель и знаменатель подкоренного выражения в (6.2.6) через G \л Н соответственно и найдем их приращения при переходе номенклатуры г из множества (кг) в множество (kr - l), т.е. за правой границей интервала:

AGnr = 2дг

Д>-1 KJ kr{kr-l) АЯпг = \rhr{kr - I) - ХгКкг =-ХгК.

Поскольку в новых обозначениях

Г* = y/G/H

(6,2.8)

(6.2.9)

L* = VGH,

(6.2.10)

уменьшение суммарных расходов после такого перехода возможно лишь при условии AG/G < \АН\/Н , или АО/АЯ < G/H. Извлекая из обеих частей последнего равенства квадратные корни и подставляя значения AG и АН , убеждаемся в его эквивалентности условию

(6.2.11)

Как видно из формулы (6.2.5), величина Тпг быстро возрастает с уменьшением кг , тогда как Т* увеличивается очень медленно. Таким

определяется последним элементом группы и получается из (6.2.5) заменой к на к + 1. Формулы для расчета приращений AG и АН принимают вид

AGnr = -

Av(Av + l)

АНпг = Xrhr. (6.2.13)

Условием целесообразности уменьшения Т с одновременным увеличением коэффициентов {кг} становятся неравенства

Приведенные соображения позволяют утверждать, что графики функций Ь{Т) и Ь[Т) имеют вид, показанный на рис. 6.1 (штриховыми линиями показаны границы постоянства группировок, пунктиром - локальные оптимумы). Они дают основания предложить следующий алгоритм планирования многономенклатурных поставок:

1) Упорядочить номенклатуры по возрастанию отношений {gi/[\ihi)} и произвести их перенумерацию.

2) Выбрать начальное приближение для базисного периода То .

3) Рассчитать для него оптимальный набор коэффициентов {к} .

4) Рассчитать значения 0,Н для этих коэффициентов по формулам (6.1.6) и (6.1.7). Вычислить Т* .

5) По формуле (6.2.5) рассчитать правые границы интервала постоянства группировок {Т\{к)} , по (6.1.12) - левые.

6) Установить в нуль указатель key направления изменения Т.

образом, выполнение условия Тпг > для всех г говорит о нецелесообразности дальнейшего увеличения Т и связанного с ним уменьшения коэффициентов {кг} , так как минимумы L* будут возрастать.

Аналогичные рассуждения могут быть проведены и для возрастающих коэффициентов {к} при движении по оси Т в сторону у1\лень-шения базисного периода. Расчетное соотношение для левой границы интервала постоянства группировок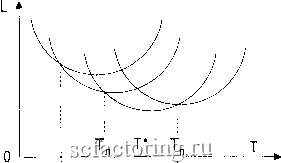

Рис. 6.1. Функция затрат и ее производная

7) Если существует такое г, что Тщ < Т* , положить key = 1 ; иначе, если существует такое г , что Тл, > Т* , положить key = - 1 .

8) Пока key = -1 : установить key = 0. Рассчитать AG и АН по всем номенклатурам, для которых {Тщ} > Т* ; найти EAG и ЕДЯ ; заменить для всех этих номенклатур ki на ki + 1 и рассчитать новые {Tni} . Вычислить новые значения G := G -\- АС, Я := Я-ЬАЯ и пересчитать по ним Т* \л L* . Если корректировки были, установить key = -1 и вернуться на начало пункта.