Таблица 6.1 Расчет системы кратных периодов

Таким образом, уже начальная группировка дала решение, практически совпадающее с оптимальным по значению целевой функции.

Описанное выше улучшенное приближение было связано с затратами 16.928 и для достижения минимума (того же) потребовало двух дополнительных шагов. Это не исключает возможного преимущества улучшенного начального приближения при других исходных данных.

Аргументами в пользу объединения заказов являются также оптовые скидки и возможное требование поставщика о стоимости каждого заказа не ниже некоторого порога. В любом случае начинать следует с реализации вышеописанного алгоритма. Если стоимость заказа по < 1 >-множеству превышает порог скидки, то расчет следует повторить с учетом скидок и на этом вычисления закончить. Иначе необходимо подсчитать стоимости заказов для каждого периода из набора в К периодов, где К наименьшее общее кратное чисел {kj} , определить

потери от упущенных скидок в единицу времени и отнести их к общим затратам на организацию поставок. Если потери существенны, необходима модификация алгоритма с целью максимизации полученных скидок [190. с. 504-505].

6.3. Взаимозаменяемые продукты

Расссмотрим двухпродуктовую модель с возможной заменой второго продукта первым. Предполагается, что на замену единицы второго продукта требуется к единиц первого и дополнительные затраты с. На рис. 6.2 представлены синхронизированные графики изменения запасов первого и второго типов для одного цикла работы системы.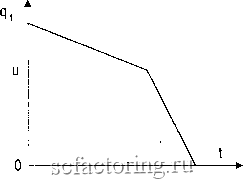

Рис. 6.2. К модели с заменой продукта

Затраты за цикл и длительность цикла удобно выразить через объем поставки q2 и остаток и запаса по первому продукту, обеспечивающий покрытие спроса по обоим продуктам после исчерпания запаса по второму. Прежде всего отметим, что 2 = Я2/2 Далее,

qi=: и + q2Xl/\2-

Расходы на хранение за цикл пропорциональны импульсу соответствующего запаса. Для второго продукта на участке [0,2] средний запас равен д2/2 , а импульс запаса - go/lAo) . На заключительной фазе цикла запас и импульс равны нулю. По первому продукту на участке [0,2] средний запас равен и плюс половина спроса за это время, что приводит к импульсу [г/-I-Ai2/(2A2)]g2/A2 . На участке [t2T] запас и расходуется за время u/{Xi-j-kX2), а средний запас равен и/2 . Импульс запаса равен u/[2(Ai -h кХ2)].

В каждом цикле выплачиваются также стоимость восполнения д и стоимость компенсации дефицита второго продукта соответствующим объемом первого по цене с. Этот объем равен пересчитанной к первому продукту потребности во втором в заключительной фазе цикла, т.е. kX2u/{Xi -f А:А2) . Таким образом, суммарные затраты за цикл

Lt = g-hcukX2/{Xi-\-kX2)-\-h2ql/i2X2)

= 9 -Ьи

Al2\ Q2

скХ2

А2 2(Ai+A-A2).

Ai -}- АгА2 А2

Для перехода к затратам в единицу времени эта сумма должна быть разделена на длительность цикла

T = g2/A2 + i (Ai + /:A2).

Оптимальные и \л q2 находятся численными методами. Чтобы получить начальные приближения, запишем функцию затрат за период Т по второй номенклатуре. В нее войдут расходы:

на содержание среднего запаса q2/2 в течение 2/2 л2<?1/(2а2);

итого