2. Основная модель

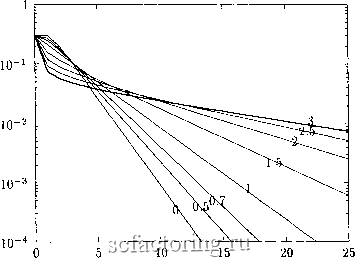Рис. 9.1. Распределение числа заявок в системе M/G/1 1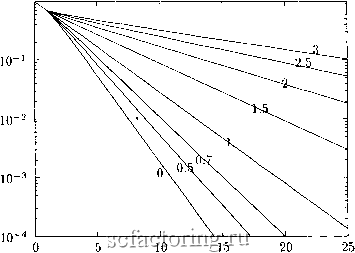

Рис. 9.2. Распределение сумм вероятностей в системе M/G/1

9.3. Многолинейная марковская система

Естественно считать s > п. В этой области согласно (3.12.2) вероятность дефицита

,5 + 1-П

Следовательно, функция затрат

L{s) = hydpn-

Приращение вероятности дефицита в случае замены 5 на 5+1

Д(1)(5) = Ь+2-п . + 1-п] р р + 1-п. (9.3.1)

Значит, оптимальный запас при известном р должен определяться из неравенств

РпР- <h/d<pnp-

откуда

HdPn/h)

L In(l/P) J

При исчислении штрафов по вероятности дефицита последняя в случае s > п вычисляется согласно

Следовательно, функция затрат

L{s) = hy-\- dpn Приращение ожидаемого дефицита

Оптимальный запас вычисляется по формуле

/fey Hi/p)

9Л. Учет дополнительных задержек

При заметной удаленности ремонтного органа следует учитывать дополнительное снижение объема ЗИПа за время Т доставки агрегата в ремонт и обратно. При простейшем потоке заявок это распределение для фиксированного Т подчинено закону Пуассона

= , = 0 .....

а для случайного с плотностью распределения v{t) считается как

Вопрос об эффективном расчете этих вероятностей рассматривался в разд. 3.6.3.

Результирующее распределение снижения ЗИПа получается сверткой распределений числа агрегатов, находящихся в транспортировке и непосредственно в ремонте. Эта рекомендация относится и ко всем моделям с восстанавливаемым ЗИПом, которые рассматриваются ниже.

9.5. Восстановление в сети

Восстановление отказавшего агрегата может потребовать ряда операций, выполняемых на специализированном оборудовании. При этом возможно совмещение ремонта нескольких агрегатов, проходящих различные фазы обслуживания. В таких случаях приходится иметь дело с сетью обслуживания, а снижение ЗИПа определяется числом заявок, находящихся в сети (включая очереди к ее узлам). Это обстоятельство, не меняя общего подхода и условий оптимальности, требует подстановки в последние распределения числа заявок в сети. Сети обслуживания рассчитываются методом потокоэквивалентной декомпозиции (см. разд. 3.15), в котором после балансировки потоков выполняется независимый расчет распределений числа заявок в узлах сети. Эти распределения нужно последовательно свернуть по узлам - см. формулу (3.4.9).