Эффект изоляции

Пытаясь упростить выбор между доступными им альтернативами, люди часто игнорируют общие компоненты альтернатив и сосредоточивают свое внимание на компонентах, которые у этих альтернатив различны. Подобный подход к проблеме выбора неминуемо ведет к появлению противоречащих друг другу предпочтений. Происходит это из-за того, что две перспективы могут быть разложены на одинаковые и различные компоненты более чем одним способом, а каждое такое разложение будет порождать различные предпочтения. Подобное отклонение Канеман и Тверски назвали эффектом изоляции.

Проблема 10. Рассмотрим следующую двухэтапную игру. На первом этапе с вероятностью 0,75 игра может закончиться, не принеся ничего, а с вероятностью 0,25 - перейти на второй этап. Если нам повезло и мы попадаем на второй этап, то сталкиваемся с проблемой выбора между двумя перспективами

(4000,08) и (3000).

Выбор одной из них должен быть сделан еще до начала игры, т. е. до того, как исход первого этапа игры станет известен.

Заметим, что в этой игре индивидуум должен выбирать между двумя перспективами: с вероятностью 0,25x0,8 = 0,2 выиграть 4000 и с вероятностью 0,25x1 = 0,25 выиграть 3000.

Таким образом, в терминах исходов и их вероятностей индивидуум должен выбрать перспективу (4000, 0,2) или (3000, 0,25). Получаем запись проблемы 4, которая уже была рассмотрена нами выще.

Несмотря на то что проблема 4 и проблема 10 эквивалентны, они порождают различные предпочтения респондентов. В проблеме 10 из 141 опрощенного респондента 78% выбрали перспективу (3000, 0,25), в то время как в проблеме 4 больщинство респондентов выбрало перспективу (4000, 0,2). Очевидно, что причиной подобного результата может быть только то, что люди полностью игнорируют в анализе первую стадию игры в проблеме 10. Они начинают рассматривать проблему 10 как проблему выбора между двумя перспективами: (3000) и (4000, 0,8). А этот выбор эквивалентен проблеме 3, рассмотренной нами выше.

Стандартное и последовательное представление проблемы 4 дано в виде дерева решений (рис. 18 и 19). Согласно общепри-116

0,25

3000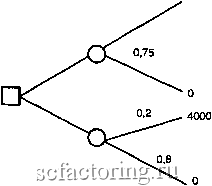

Рис, 18. Стандартное представление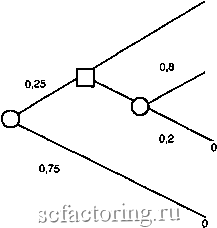

3000

4000

Рис. 19. Последовательное представление

В стандартном представлении (рис. 18) индивидуум стоит перед проблемой выбора между двумя рискованными перспективами, в то время как в последовательном представлении

нятому подходу квадраты обозначают узлы, в которых решения принимаются индивидуумом, а круги - узлы, в которых решение зависит от шанса.

Основное различие между рис. 18 и 19 заключается в местоположении узлов, в которых решения зависят от индивидуума.

(рис. 19) - перея проблемой выбора между рискованной и безрисковой перспективой. Это различие дополняется введением в анализ взаимосвязи между перспективами, которая никак не связана с изменением их вероятностей или исходов. Например, в случае с последовательным представлением событие не выиграть 3000 содержится в событии не выиграть 4000 , а в стандартном представлении эти два события абсолютно не связаны между собой. Таким образом, исход с выигрышем 3000 в последовательном представлении имеет некоторые (мифические) преимушества по сравнению со стандартным представлением.

Подобные повороты предпочтений [reversal of preferences], возникающие в результате взаимосвязи событий, грубо нарушают одно из основных следствий теории рационального поведения, которое гласит: выбор между перспективами должен проводиться только и только на основе исходов и вероятностей их реализации.

Итак, если суммировать все вышесказанное, то эффект изоляции приводит к тому, что безрисковая перспектива, приносящая какую-то фиксированную прибыль, выглядит в глазах большинства индивидуумов намного привлекательней, чем рискованная перспевсгива, которая предоставляет ту же прибыль с той же вероятностью.

Теперь, после того как мы разобрались с тем, какое влияние на предпочтения индивидуумов оказывают различия в представлении вероятностей, посмотрим, какое влияние на предпочтения индивидуумов оказывают различия в представлении исходов. Проблемы 11 и 12 - отличные примеры таких влияний.

Проблема 11. К вашему текущему благосостоянию прибавили 1000. Теперь вас просят сделать выбор между двумя альтернативами:

А: (1000, 0,5) В: (500)

[16] [84]

Проблема 12. К вашему текущему благосостоянию прибавили 2000. Теперь вас просят сделать выбор между двумя альтернативами:

С: (-1000, 0,5) D: (-500)

[69] [31]

Большинство респондентов выбрало перспективу В в проблеме 11 и перспективу С в проблеме 12. Подобные предпочте-