Рисунок 8.2. Процентные изменения доходности казначейских векселей и соответствующие изменения цен фьючерсов на S&P 500 на будущий год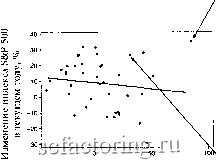

Изменение доходности казначейских векселей в предыдущем году, %

y = 2,3%-i(x) = 2,3%

Источник: Standard & Poors Security Price Index Record

фондового рынка в следующем. Первое, что нужно сделать, - собрать данные об этих переменных.

Мы собрали по каждой переменной данные за 39 лет и отобразили каждую пару значений на графике, приведенном на рис. 8.2. Стрелки, которые идут от цифр в таблице к графику, показывают, где на нем отображена данная пара значений переменных. Они указывают на 1995 и 1980 годы, когда и процентные ставки, и темпы роста акций были исключительно высокими.

Принято на вертикальной оси помещать ту переменную, поведение которой предсказывается, а на горизонтальной - переменную-предсказатель. Их совместные значения отображаются на графике точками, крестиками, какими-нибудь другими графическими символами или буквами.

Если визуально облако точек вытянуто из нижнего левого в правый верхний угол, это признак прямой (положительной) зависимости, что означает:

Высоким значениям одной переменной соответствуют высокие значения другой переменной.

Средним значениям одной переменной соответствуют средние значения другой переменной.

Низким значениям одной переменной соответствуют низкие значения другой переменной.

Если облако точек вытягивается из верхнего левого угла в нижний правый - это признак негативной корреляции. В этом случае, когда первая переменная принимает высокие значения, вторая принимает низкие и т. д. Если облако рассеивания бесформенное, это означает, что никакой связи между двумя переменными нет.

В нашем примере диаграмма показывает негативную корреляцию между процентными ставками в данном году и ценами на акции в следующем году.

Диаграмма рассеивания дает первое впечатление о взаимозависимости, но анализ можно продолжить. Следующий

шаг - провести ряд вычислений, которые основаны на отклонениях (или дисперсии) значений каждого наблюдения от средних величин. Цель этой процедуры - определить, насколько тесна взаимосвязь.

Для начала данные можно сгруппировать в четырехклсточной (2 X 2) таблице, в зависимости от того, ниже они или выше средних. В нашем примере среднее значение для изменения акций 8,9%, а для изменения ставок - 5,2% (табл. 8.1).

Обратите внимание, что в 15 случаях изменения двух интересующих нас переменных соответствовали друг другу, т.е. отличались от среднего в этом направлении, а в 24 случаях - были обратными, т. е. если одна переменная превышала среднее, то другая была ниже среднего. Приемлемая быстрая оценка величины взаимосвязи - это разница между количеством соответствующих и несоответствующих по разнице со средним значением пар, поделенная на количество наблюдений. В нашем случае это равно:

Полученное значение -0,23 - это грубая оценка корреляции, которая изменяется от +1 (максимальное значение), если в 100% случаев отклонения от среднего по направлению будут соответствовать друг другу, до -1 (минимальное значение), если, напротив, во всех случаях они будут разнонаправленными.

Отрицательная корреляция показывает обратную связь между процентными ставками и изменениями индекса S&P.

Для того чтобы построить таблицу 2x2, проведите горизонтальные прямые через среднее значение по горизонтали и через среднее значение по вертикали. Эти две прямые поделят график на четыре квадранта. Потом подсчитайте количество наблюдений в каждом квадранте и поместите результаты в таблицу.