ЧАГТЬУ! Оп.тпны

акции. Опцион на акции, изменение цен на которые более чем на 1 или 2% маловероятно, имеет небольшую стоимость; опцион на акции, цена на которые может упасть или вырасти в два раза, имеет очень большую ценность.

Графики (а) и (б) на рисунке 20-9 поясняют вышесказанное. На них сравниваются доходы при исполнении двух опционов с одинаковыми ценами исполнения и с одинаковой ценой акции. Графики основаны на допущении, что цена акции равна цене исполнения (как в точке Сна рисунке 20-8), хотя это не обязательное допущение. Единственное отличие состоит в том, что предсказать цену акции Y на дату исполнения опциона по ней (рисунок 20-9(5) гораздо труднее, чем цену акции X на дату исполнения опциона по ней. Вы можете это видеть при наложении на рисунки кривых распределения вероятностей.

В обоих случаях существует 50%-ная вероятность, что цена акций снизится и опцион потеряет стоимость, но если цены на акции X и У поднимутся, то, вероятно, цена акций Y вырастет больше, чем цена акций X. Таким образом, существует крупный шанс больших доходов от опциона на акции Y. Поскольку вероятность нулевых доходов от обеих акций одинакова, опцион на акции Y стоит больше, чем опцион на акции X. Рисунок 20-10 иллюстрирует это: кривая, представляющая опцион на акцию Y, расположена выше.

Вероятность крупных изменений цен на акции до истечения срока исполнения опциона зависит от двух вещей: 1) дисперсии (т.е. изменчивости) цен на акции за один период и 2) количества периодов до истечения срока опциона. Если до истечения срока опциона осталось ? периодов, а дисперсия цены за период равна а\ то стоимость опциона определяется кумулятивной изменчивостью at. При прочих равных условиях для вас предпочтительнее было бы иметь опцион на акцию с изменчивыми ценами (с высоким значением а). При данной изменчивости для вас предпочтительнее было бы иметь опцион с более длительным сроком исполнения (большое значение t). Итак, стоимость опциона возрастает с увеличением как изменчивости цены акции, так и срока его исполнения.

РИСУНОК 20-10

Стоимости опционов колл на акции фирм X и Y. Опцион колл на акции Y стоит больше, поскольку цена акций фирмы Y более изменчива (см. рисунок 20-9). Верхняя кривая представляет стоимость опциона колл на акцию Y; нижняя - стоимость опциона колл на акцию X.

Стоимости опционов колл на акции фирм XhY

Верхняя граница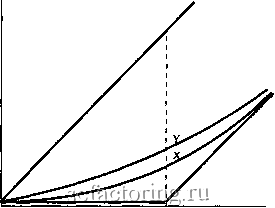

Нижняя граница

Цена акции

Цена исполнения

10 Интуитивное объяснение. Если цена акции изменяется случайным образом (см. раздел 13-2), последовательные изменения цены статистически независимы. Обшее изменение цены до истечения срока исполнения опциона равно сумме t случайных переменных. Дисперсия суммы независимых случайных переменных равна сумме дисперсий этих переменных. Итак, если а является дисперсией ежедневного изменения цены и до истечения срока исполнения осталось / дней, дисперсия обшего изменения цены равна а

Почему принцип Принятый нами метод оценки, включаюший в себя: 1) прогнозирование ожи-дискоитирован- Даемых потоков денежных средств и 2) дисконтирование их по ставке, равной ного денежного альтернативным издержкам, не подходит для оценки опционов. Первая часть потока не запутанна, но выполнима. Определить же точную величину альтернативных из-

подходит для держек невозможно, поскольку риск опциона изменяется при каждом изме-оценки опционов нении цены акции , и мы знаем, что он будет меняться случайным образом в течение жизни опциона.

Когда вы покупаете опцион колл , вы открываете позицию с акцией, но тратите своих денег меньше, чем если бы покупали акцию непосредственно. Поэтому опцион всегда сопряжен с ббльшим риском, чем лежащие в его основе акции. Он имеет более высокую бету и более высокое стандартное отклонение дохода.

Насколько риск опциона выше, зависит от отношения цены акции к цене исполнения. Опцион в деньгах (когда цена акции выше цены исполнения) надежнее, чем опцион вне денег (цена акции меньше цены исполнения). Таким образом, рост цен на акции увеличивает цену опциона и снижает свойственный ему риск. Когда цена на акции падает, цена опциона также падает.

Риск также изменяется со временем, даже если цена акции остается постоянной.

ТАБЛИЦА 20-2

От чего зависит цена опциона колл

1. Если следующие переменные

возрастают: изменения цены опциона колл :

Цена акции (Р) положительное

Цена исполнения (ЕХ) отрицательное

Процентная ставка (/) положительное

Срок исполнения опциона {t) положительное

Изменчивость цены акции (о) положительное

2. Другие характеристики:

а) Верхняя фаница. Цена опциона всегда меньше цены акции.

б) Нижняя граница. Цена опциона никогда не упацет ниже стоимости немедленного исполнения опциона (/ - ЕХ или О, в зависимости от того, что больше).

в) При обесценивании акции опцион также теряет стоимость.

г) По мере возрастания цены акции до очень большой величины цена опциона приближается к цене акции за вычетом приведенной стоимости цены исполнения.

Примечание. Прямое влияние на цену опциона увеличения значений или а положительно. Но их увеличение может оказывать и косвенное влияние. Например, рост может снизить цену акции Р. Это, в свою очередь, может снизить цену опциона.

Мало кто способен сразу усвоить все эти особенности при первом прочтении. Поэтому мы в обобшенном виде представили их в таблице 20-2.

20-4. МОДЕЛЬ ОЦЕНКИ СТОИМОСТИ ОПЦИОНОВ

Теперь мы хотели бы вместо качественных характеристик, представленных в таблице 20-2, дать строгую модель оценки стоимости опционов - формулу, в которую мы можем подставить числа и получить определенный ответ Поиск этой формулы занял многие годы, пока Фишер Блэк и Мирон Шольц не вывели ее. Прежде чем мы покажем, что они обнаружили, мы должны сказать несколько слов о том, почему поиск формулы был сопряжен с такими трудностями.

а присущий ему риск возрастает. Поэтому требуемая инвесторами ожидаемая норма доходности опциона изменяется ежедневно или ежечасно, всякий раз, когда меняется цена акции.

Мы повторим общее правило: чем выше цена акции относительно цены исполнения, тем надежнее опцион, хотя опциону всегда сопутствует более высокий риск в сравнении с акциями. Риск опциона меняется каждый раз, когда меняется цена акции.

Создание эквивалентов опциона из обыкновенных акций и займов

Если вы усвоили все, о чем мы говорили до этого, вы можете понять, почему трудно оценить стоимость опциона, используя стандартные формулы дисконтирования потоков денежных средств, и почему экономисты долгие годы не могли найти точных методов оценки опционов. Крупное открытие было ознаменовано восторженным возгласом Блэка и Шольца: Эврика! Мы нашли ее!О Вся хитрость в том, чтобы создать эквивалент опциона из комбинации инвестиций в обыкновенную акцию и получения займа. Чистые затраты на приобретение эквивалента опциона должны равняться стоимости опциона .

Мы покажем вам, как это делается, на простом числовом примере. Мы определим стоимость опциона со сроком 1 год, дающего право на приобретение акций корпорации Вомбат по цене исполнения 110 дол. Чтобы упростить задачу мы сделаем допущение, что с акциями Вомбата в предстоящем году могут произойти только две вещи - их стоимость либо снизится со 110 до 80 дол., либо вырастет до 125 дол. Также мы допустим, что краткосрочная процентная ставка равна 10%.

Если цена на акции Вомбата упадет до 80 дол., опцион колл потеряет стоимость, но если она поднимется до 125 дол., то опцион будет стоить 125-110=15 дол. Опцион может дать следующие доходы:

Цена акции = 80 дол. Цена акции = 125 дол.

Один опцион колл

О дол.

15 дол.

Теперь сравним эти доходы с доходами, которые мы получили бы, купив одну акцию и взяв заем в банке в размере 72,73 дол.:

Заметим, что доход от инвестиций в акцию с использованием займа идентичен доходам от m/jex: опционов колл . Следовательно, оба вида инвестиций должны иметь одинаковую стоимость:

Стоимость трех опционов колл = стоимость акции - банковский заем= = 100- 72,73 =27,27дол.

Стоимость одного опциона = 9,09дол. Гопля! Вот мы и оценили стоимость опциона колл .

Мы, правда, не знаем, сидели ли Блэк и Шольц в тот момент в ваннах, подобно Архимеду