зависимость всего временного ряда, в то время как такая зависимость может проявляться только в отдельные интфвалы времени. Например, для очень больших временных интервалов, как мы демонстрируем ниже, эта особенность будет убираться глольной усредняющей процедурой.

DJIA

2800

2600

2400

2200

2000

1800

1600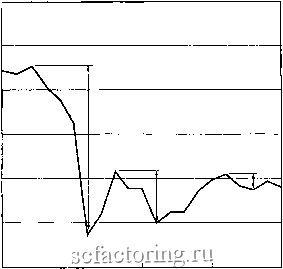

1987.77 1987.79 1987.81 1987.83

Time (decimal years)

1987.85

Рис. 21. Определение просадки. Пример краха, который произошел 19 оетября 1987, показывает три просадки, соответствуюцие совокупным потерям от последнего (прошлого) максимума до следуюцего минимума цены. Самая большая просадка с полной потерей -30.7% состоял из четырех последовательных ежедневных снижений: 14 октября 1987 (1987.786 в десятичных годах), DJIA-индекс - упал на 3.8%; 15 октября рынок упал на 6.1%; 16 октября рынок просел на 10.4%. После уик-энда и падения в Черный понедельник 19 октября 1987 получается совокупная потеря или просадка на 30.7%. В терминах последовательных ежедневных потерь, это создает ряд 3.8%, 2.4%, 4.6% и 22.6% (обратите внимание, что возврацения не просто суммируются, так как они - ценовые изменения, нормализованные по цене, которая сама изменяется).

Нелинейная модель с нулевой корреляцией, но высокой предсказуемостью. Чтобы лучше понять, как измерять с помощью просадок едва различимые зависимости в последовательных вариациях цены, давайте сыграем в следующую игру, в которой приращение цены определяется правилом:

5p(t) = E(t) + £(t-l)£(t-2) (5)

где E(t) - процесс, назьшаемый белым шумом с нулевой модой и единичной дисперсией. Например, £(t) может бьтть равно либо +1 или -1 с вероятностью 1/2. Определение (5) означает, что сегодняшнее приращение цены контролируется тремя случайными бросками монеты - один бросок для сегодня , один - для

вчера и один - для позавчера . Очевидно, что положительный бросок монеты сегодня, а также два положительных броска вчера и позавчера означают движение цены вверх. Аналогично, отрицательный бросок сегодня, а также два различных броска вчфа и позавчфа, двигают цену вниз.

Легко провфить, что среднее E(6p(t)), а также двухточечная корреляция E(Sp(t),5p(t)) для 1фг равна нулю и, таким образом, dp(t) также является белым шумом. Интуитивно, такой вьшод возникает из того факта, что в эту характеристику временного ряда вводится нечетное число бросков монеты, чье среднее равняется нулю ((1/2) X (+1) + (1/2) X (-1) = 0). Однако, трёхточечная корреляционная функция E(Sp(t - 2) 8p(t - 1) ф(ф не равна нулю, но равна 1 и ожидание величины ф(4 требующее знания двух предыдущих приращений ф(if - 2) и фС - i) не равно нулю, а равно E(Sp(t) Sp(t -2), ф(Г -l))=6p(t - 2)Sp{t -1). Это означает, что возможно предсказать изменение цены сегодня с большей, чем 50% вероятностью, если знать изменение цены вчфа и позавчера!

В то время, как частота распределения приращений цен и двухточечная функция корреляции строятся для этой сфуктурной зависимости, распределение просадок показьгоает специфическую характфистику временного ряда. Для упрощения анализа и четкости понимания, давайте снова офаничимся случаем, когда £ (t) может принимать лишь два значения ±1. Тогда 5p(t) может принимать только фи значения О и ±2 и соответственно:

где левая колонка дает фи последовательных значения e(t-2), £(t -1), e(t), а правая колонка - соответствующее приращение цены С помощью этой четкой консфукции мы явно видим, что (t) - это белый шум. Таким образом, существует явная предсказуемость и распределение просадок офажает это: не существует просадок длительностью больших, чем два шага (интфвала) времени. В самом деле, самая худшая из тозможньк просадок соответствует следующей последовательности е: - + -. Это соответствует последовательности приращений цены +2, -2, -2, которая либо останавливается на +2, если последующее £ это +, или последовательностью нулей, прфванной появлением +2 при перюм е = +. В то время, как просадки процесса eft) мотут, в принципе, бьтть бесконечной длительности, просадки p(t) таковыми бьтть не мотут. Это показывает, что структура процесса dp(t) определяемого (5) имеет драматическую характеристику в распределении просадок в p(t). Этот факт иллюсфирует то, что просадки являются более адекватной и эластичной к масштабу времени,

характеристикой ценоюго движения, чем еженедельные или ежедневные приращения, или любые другие приращения на фжсированной временном масщтабе.

JtpocadKVL и выявление выбросов

Чтобы лучще продемонстрировать новую информащпо, содержащуюся в просадках и сравнить ее с приращениями на фиксированном временном масиггабе, рассмотрим гипогегическую ситуащпо краха на 30%, происходящего за три дня тремя последовательными падениями, каждое, в точности равное 10%. Таким образом, крах определяется как общее падение или просадка на 30%. Вместо того, чтобы рассматривать просадки, последуем общему подходу и исследуем ежедневные данные, в частности, распределение ежедневных приращений. 30% просадка теперь видится как три ежедневньж падения на ЮУо. Важно понимать, что в построении распределения ценовых приращений учитьшаегся лшиь количестю дней, в течение которых данное приращение было наблюдаемо. Таким образом, крах будет состоять из трёх дней с 10% снижением цен, опуская информацию о том, что три падения произошли последовательно! Чтобы увидеть к чему может привести потеря данной информации, рассмотрим рынок, на котором падение на 10% в течение одного дня, обычно, происходит раз в четыре года (это довольно правдоподобные цифры для индекса Nasdaq-композит в нынешние времена высокой волатильносги). Считая, что в году приблизительно 250 торговых дней, имеем 1000 рабочих дней и одно событие в течение этого периода. Таким образом, это соответствует вероятности такого исхода (дневного падения на 10%) 1/1000=0.001. Крах на 30% получается рассеченным на три собьпия, которые не столь примечательны (каждое с относительно коротким средним временем повторения равным четырем годам). Какова вероятность трех последовательных падений на 10% в течение дня согласно данному описанию? Простая теория вероятности говорит нам, что это будет вероятность одного дневного падения на 10%,умноженная на вероятность одного дневного падения на 10% и снова умноженная на вероятность одного дневного падения на 10%. Правило расчета вероятности сохраняется, если три события рассматривается как независимые. Эти расчеп>1 дакгт 0.001x0.001x0.001= 0.000,000,001=10 . Это соответствует одному случаю на 1 миллиард торговых дней! Мы должны, таким образом, ждать приблизительно 4 миллиона лет, чтобы быть свидетелем такого события!

Что же пошло не так, как надо? Просто, взгляд на дневные приращения и их распределение разрушил информацию о том, что такие исходы могут быть коррелированны в определенные времена! Этот крах походит на мамонта, который был рассечен на части без сохранения сведений о связях между частями, и нам оставили то, что напоминает мьш1ей (такое небольшое преувеличение)! Наша оценка события из трёх последовательных потерь по 10% как невозможного, основывалась на неправильной гипотезе о том, что эти три события являются независимыми. Независимость между последовательными ценовыми приращениями - хорошо проверенный факт для большей части времени. Однако, может быть большие падения не являются независимыми. Другими словами, может быть, существуют вспышки зависимости , или, гоюря по-другому, отрезки

предсказуемости .

Очевидно, что просадки будут содержать точную информацию, относящуюся к идентификации юзможной юпьшжи местной зависимости, ведущей к необычайно большим совокупным потфям.

Ожудаемое распределение нормальныnpocadot{

Перед тем, как вернуться к данным, мы должны спросить себя о том, что можно ожидать на основе гипотезы случайных блужданий. Если ценовые изменения независимы, положительные (+) и отрицательные (-) шаги следуют друг за другом подобно орлам и решкам рыночного броска монеты. Для симметричных распределений ценовых изменений, начинающихся с плюса, +, вероятность получить минус, -, равна 1/2. Вероятность получить два минуса в ряду -1/2x1/2=1/4; вероятность получить три минуса в ряду - 1/2 х 1/2 х 1/2 = 1/8, и так далее. Для каждого дополнительного отрицательного приращения мы видим, что вероятность делится надвое. Это определяет так называемое экспоненциальное распределение, описывающее тот факт, что увеличение длительности просадки на одну единицу времени делает ее вдвойне менее вероятной. Этот показательный закон также известен, как закон Пуассона и описывает процессы, не имеюцще

памяти: для последовательности +----, тот факт, что четыре минуса произошли

кряду, не изменяет вероятность для ноюго события, которая остается равной 1/2, и для плюса, и для минуса. Такой не имеющий памяти процесс может казаться протиюречащим интуиции (множестю людей предпочли бы ставить на решку после последовательности из десяти орлов, что часто именуется ошибкой азартного игрока ), но он точно отражает то, что мы подразумеваем под полной случайностью: в справедливом броске монеты, может случиться так, что выпадут десять орлов кряду. Одиннадцатое событие по-прежнему имеет вероятность 1/2 того, что вьшадет орел. Отсутствие памяти в таких случайных процессах может бьпъ постулировано следующим образом: учитывая прошлое наблюдение из п последовательных минусов, вероятность для следующего минуса не изменяется от безусловного значения Ш, независимо от величины п. Любое отклонение от этого показательного распределения просадок будет сигнализировать о некоторой корреляции в процессе и, таким образом, о возможности предсказания будущих событий.

Поскольку, в случайной модели без памяти, существует больше половины просадок с продолжительностью большей, чем один временной период, то удобно визуализировать эмпирическое распределение этих просадок на рьшке акций в логарифмическом масштабе, где ожидаемое показательное распределение становится прямой линией. Это весьма эффекгавный метод проверить действительность гипотезы: отклонения от прямой линии будут сигнализировать некоторое отклонение от показательного распределения и, таким образом, от гипотезы об отсутствии памяти.

Свидетельства, представленные ниже, относительно наличия выбросов ю временном ряду ценовых приращений не полагаются на справедливость этого закона Пуассона. Фактически, мы уже идентифицировали небольшие отклонения от него в распределении просадок, что предполагает необходимость отхода от

гипотезы независимости между последовательными ценовыми приращениями. Это ведет нас к весьма тонкому пункту, который избежал внимания даже многих из самых умньж наптих коллег в течение определенного времени и все еще не привлекает внимания больщинства других. Этот тонкий пункт состоит в том, что свидетельство наличия в выборке ценовых приращений выбросов и чрезвычайньж событий не требует и, даже вообще не синонимично существованию сколь-нибудь заметного провала в распределении просадок. Позвольте наглядно и убедительно проиллюстрировшъ это утверждение, позаимствовав аналогию го другой области активных научных исследований, а именно, из исследований сложности водоворотов и вихрей в турбулентных потоках жидкости, типа горных речек или атмосферной завихрений. Поскольку рещение точных уравнений для этих потоков не представляется возможным, то полезный подход должен был упростить проблему до изучения простых игровых моделей, типа, так назьшаемых корпусных моделей турбулентности, которые, как полагают, описьшают существенные компоненты таких потоков и в то же время поддаются анализу. Такие корпусные модели заменяют трехмерную пространственную область рядом однородных сферических слоев, наподобие луковицы, с радиусами, увеличивающимися, как геометрический ряд 1, 2, 4, 8..., 2п и сообщающимися между собой, главным образом, только с самыми близкими соседями.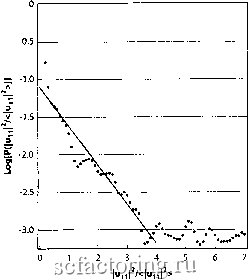

Рис. 22. Функция распределения вероятности квадрата скорости жидкости, нормализованная к ее среднему времени, в одиннадцатом слое ифовой модели гидродинамической турбулентиости, обсуждаемой в тексте. Вертикальная ось имеет такой логарифмический масштаб, чго прямая линия, которая помогает глазу, квалифицируется, как очевидное показательное распределение. Обратите внимание на появление чрезвычайно редких и больших взрывов скоростей на фаю, выше экстраполяции прямой линии. Источник [25.

Что касается финансовьж временньж рядов, то большой шгтерес представляет распределение скорости изменетшй между двумя мгноветшями в той же самой позиции или между двумя точками одновременно. Такое распределение для квадрата скорости изменений показано Рис. 22. Обратите внимание на аппроксиматщю экспоненциального снижения, представленную прямой линией и на сосуществование больших колебаний справа для значений от 4 до 7 и далее, (которые не показаны). Обычно, такие большие колебания считаются статистически не значимыми и не добавляют никакого дополнительного понимания. Здесь можно показать, что эти большие колебания скорости жидкости соответствуют интенсивным пикам, когерентно распросфаняющимся через несколько корпусньк слоев с колоколообразной характфистикой, почти независимой от их амплитуды и продолжительности (даже при перемасштабировании их размера и продолжительности). При продлении наблюдений на значительно более длинный период, чтобы аномальные флуктуации, большие значения 4 на Рис. 22 могли бы бьггь смоделированы намного лучше, мы получаем непрфьшные фивые (кроме некоторого постоянного остаточного шума), показанные на Рис. 23. Здесь, каждая из фех фивьж соответствует измерению распределения в данном корпусном слое (п = И, 15, и 18).

На Рис. 23 было вьтолнено стандартное преобразование, при котором сжимались или растягивались абсцисса и ордината для каждой фивой таким образом, чтобы все фи фивые совпали друг с другом. Если такое преобразование окажется успешньм, то это будет означать, по определению, что эти фи распределения идентичньт Этот факт очень полезен для понимания лежащего в основе механизма, а также для использования в будущем при оценивании риска и управлении им. Наивно было бы ожидать, что одинаковая физика применима в каждом из сффических слоев и что, как следствие, распределения должны быть одинаковыми, если не юменять единицу длины разяичньж масштабов, существующих в каждом слое. Здесь, мы наблюдаем, что фи фивые действительно замечательно совпадают, но только для маленьких флуктуации скорости, в то фемя как большие колебания описываются очень разными толстыми хвостами. В противном случае, если попьггаться свести фивые в области больших колебаний скорости, тогда части фивьж, близких к началу (в области мальк скоростей) не сходятся вообще и очень различньт Отсюда можно сделать заключение -распределения приращений скорости, по-видимому, состоят ю двух областей: области, так назьшаемьк нормального масштабирования и области эксфемальных событий.

Вывод, который проистекает из приведенного вьш1е обсуждения: концепция выбросов и эксфемальньж событий не фебует, чтобы распределение было не гладким, как показано на правой части Рис. 22. Шум да и, в особенности, сам процесс построения распределения будут почти всегда сглаживать фивые. В [252] найдено, что это распределение состоит из двух различньк совокупностей событий, тела и хвоста, которые имеют различную физику, различный масштаб и различные свойства. Это явная демонсфация того факта, что модель турбулентности содфжит выбросы , которые фактуются как четкая фуппа очень больших и весьма редких событий, которые пфемежают нормальную динамику и которые не могут быть