Когда коэффициент риска становится равным 2, мы предполагаем, что темп прироста удваивается до 2% и остается неизменным до тех пор, пока коэффициент риска снова не удвоится, достигнув 4. Это новое время удвоения коэффициента риска, примерно равно 1/0,02=50 дням при этом 2%-ом темпе роста. Когда коэффициент риска достигает 4, его темп прироста удваивается до 4%. Время удвоения коэффициента риска, таким образом, делится пополам до 25 дней, и продолжается аналогичный сценарий: с удвоением темпа прироста каждый раз удваивается коэффициент риска. Поскольку удвоенное время делится примерно пополам на каждом этапе, мы имеем следующую последовательность (время=0, коэффициент риска=1, темп прироста =1%), (время=100, коэффициент риска=2, темп прироста =2%), (время=150, коэффициент риска=4, темп прироста =4%), (время=175, коэффициент риска=8, темп прироста =8%), и так далее. Мы наблюдаем, что временной интервал, необходимый для удвоения коэффициента риска стремительно сокращается в 2 раза на каждом этапе. Точно так же, как в прославленном древними феками парадоксе Зенона

1111

-+ +-+--+... = 1, 2 4 8 16

бесконечная последовательность удвоений, таким образом, занимает конечное время, и коэффициент риска достигает бесконечности в конечное критическое время , примерно равное 100+50+25+... =200 (точная математическая обработка требует формулировки понятия непрерывное время , но не меняет качественного содержания примера). Спонтанная сингулярность была создана увеличивающимся темпом роста! Данный процесс является довольно общим и применим в тех случаях, как только темп прироста приобретает свойство умножаться на некоторый множитель, больший 1 в то время, как коэффициент риска ти любую другую наблюдаемую величину умножают на некоторую постоянную величину, большую 1. Мы вернемся к этому примеру в главе 10, когда будем анализировать мировую демофафическую ситуацию, основные финансовые индексы и мировой валовой экономический продукт на несколько веков вперед и попытаемся предсказать, что будет. Резюмируя все вышесказанное, мы создали модель, в которой цена фондового рынка управляется уфозой краха, измеряемой коэффициентом риска. В свою очередь, силы подражания и стадности управляют коэффициентом риска. Когда сила подражания приближается к критическому значению, коэффициент риска краха отклоняется с характерным для степенной зависимости поведением. Это ведет к специфическому степенному ускорению рьшочной цены, вооружая нас первой предварительной моделью предсказания краха. Подражание среди агентов, ведущее к росту коэффициента риска краха, может возникнуть, например, в связи с профессивным изменением уверенности инвесторов в ликвидности рынка, без привлечения асиммсфичной информации, и независимо от поведения цены и ее отклонения от фундаментальной стоимости [132].

Результаты наших исследований показывают что для описания рынка (если под рынком понимать динамику одного актива) достаточно семи-десята переменных. Что следует из оценки корелпяционного интефала системы и полученной на основе этого оценки вложенной размерности.

Интересующимся предлагаем обратится к работе Grassberger, Procaccia, 1984 Dimentions and entropies of strange attractors drom a fluctuating dynamics approach , Phisica, 13D:34, в которой описан метод и апгоригм его реализации, позволяющий по одной наблюдаемой траектории системы востстанавпивать ее мерность. Ее мерность (мерность фазового пространства), (прим. научн. ред)

Модель, управляемая ценой

Модель, управляемая ценой, инвертируют логику предыдущей модели, управляемой риском: в ней, как и в предьщущей модели, в результате действий рационапьньтх инвесторов, скорее цена управляет коэффициентом риска краха, а не наоборот. Сама цена управляется подражанием и стадностью шумовьтх инвесторов.

Как и раньше, чтобы передать взаимодействие между возрастающим усилением подражательного поведения, контролируемым связями и взаимодействием между трейдфами, и повсеместностью идиосинкразического поведения, а также влиянием многих других факторов, неподдающцхся детальному моделированию, необходимо стохастическое описание. Вследствие этого, динамика цен является стохастической, а момент реализации краха, являясь неопределенным, может характеризоваться его коэффициентом риска h(t), определяемым как вероятность в единицу времени того, что крах произойдет в следуюищй момент, если еще не произошел.

Лодрсрк;ание и стадношъ управляют рьточиой ценой

Хсийя (Hsieh) подчеркивал, что свидетельства, представленные в главе 2, подтверждают отсутствие корреляции между изменениями цены и высоким постоянством волатильносги (то есть амплитудой изменений цены), когда их совместно анализируют. Это не может бьпъ объяснено никакой линейной моделью [201, 202]. Напомним, что линейная модель описывает зависимость, в которой следствие или результат пропорционален причине, его вызвавшей. Нелинейность является обобщением линейной зависимости, описывая такой тип зависимости между причиной и результатом, который существенно более сложен. Нелинейность - это ишредиент хаоса, понятия теории сложных систем, которая интенсивно развивалась в течение нескольких последних десятилетий как возможное описание сложности мира. Теория хаоса, в настоящий момент, широко популяризирована и некоторые исследователи даже отстаивали точку зрения, что он является полезным описанием для фондовых рьшков. Это, однако, остается лишь сильным упрощением, поскольку теория хаоса основывается на предположении, что только несколько основных пфеменных взаимодействуют нелинейно и создают сложные траектории. В действительности фондовому рьшку нужно много переменных, чтобы обрести достаточно точное описание. На техническом жаргоне фондовый рьшок имеет много степеней свободы, в то время как теория хаоса фебует только нескольких. Существование множества степеней свободы является важным

предположением, используемым для моделей коллективного поведения, которые демонстрируют наличие критических точек, описанньгх. в предыдущем разделе и в главе 4. Здесь мы остановимся только на очень общем наблюдении, позволяющем утверждать, что мир и фондовый рьшок являются нелинейными системами, которое основано на более сложной зависимости, чем простая пропорциональность, между причинами и следствиями.

В научной среде широко известна шутка на эту тему: нелинейность сравнивается с не-слоном - все создания, кроме слонов , являются не-слонами . Сходство заключается в том, что большинство систем и явлений в окружающем нас мире нелинейны, за малым исключением. Вопреки этому, в школе нас учат лтшейному мьшшеншо, что очень плохо, с точки зрения нашей готовности к восприятию всепроникающей нелинейности Вселенной, будь то ее физические, биологические, психологические или социальные аспекты. Нелинейность концентрирует в себе одну из основных сложностей познания окружающего мира: поскольку следствия, в общей своей массе, не пропорциональны причинам, две причины, при взаимодействии, не аддитивны, то есть следствия являются более сложными, чем простая суперпозиция, функциями причин. То есть, результат, получающийся в результате присутствия и воздействия двух причин, действующих одновременно, не является суммой результатов, полученных в присутствии каждой из причин в отдельности, при отсутствии другой причиньт

Общепринято, среди создателей моделей финансовых рьшков, представлять вариацию цен в течение элементарного временного периода как результат воздействия двух факторов: детерминированного мгновенного приращения и случайного приращения. Первый фактор включает в себя компенсацию за предполагаемый риск, а также действие на цену таких причин, как подражание и стадность. Второй фактор включает в себя шумовой компонент ценовой динамики с амплитудой, назьшаемой волатильностью. Волатильность также может представлять собой систематический компонент, управляемый подражанием, а также многими другими факторами. Если первый фактор формирования цены отсутствует, а волатильность постоянна, то второй член сам по себе создает траектории случайных, блужданий, огшсанные в главе 2. Введение в модель вездесущей нелинейной зависимости волатильности и определенного мгновенного приращения от прошлых значений волатильности и доходностей дает нам великое множество всевозможных траекторий. Здесь нам интересны многочисленные возможные механизмы, ведущие к нелинейной положительной обратной связи цен с самими собой. Например, неточная информация и перенос риска с инвесторов на кредитуемые банки могут заставить инвесторов поднимать цены спроса на актив в большей степени, чем они хотели бы заплатить в случае, если бы полностью несли все потенциальные убытки [3]. Мы вернемся к интуитивному описанию других механизмов в главах 7 и 8.

Яриращент цтупраахяпт кдэффицшнтомрищ крсца

Ранее в данной главе мы показали, что условие отсутствия арбитража совместно с рациональными ожиданиями предполагает, что ценовые изменения от сегодняшнего к завтрашнему дню, должны точно компенсировать средние убытки в

связи с вероятностью краха. Сейчас мы рассмотрим данное равновесие в инвертированной логике: шумовые инвесторы видят, что рьшочная цена растет, они говорят на эту тему друг с Дфугом, сбиваются в стадо , покупают все больше и больше акций, подталкивая цены и дальше вверх. Поскольку изменение цены ускоряется, условие отсутствия арбитража совместно с рациональными ожиданиями подразумевают, что здесь должен присутствовать скрьпый риск, еще не отраженный в ценовой динамике, что оправдьшает эти очевидные езду без билета и бесплатный обед . Фундаментальная логика здесь состоит в том, что условие отсутствия арбитража совмесгао с рациональными ожиданиями автоматически подразумевают значительный рост риска, надвигающегося каждый раз, когда цена существенно растет, как это бьшает при созревании спекулятивного пузыря. Это вьшод, к которому придут рациональные трейдеры. Данное явление может бьтть резюмировано следующей расхожей в среде трейдеров фразой, применимой к растущему рьшку спекулянтов, играющих на повьшяение ( бычьему рынку ): Это слишком хорошо, чтобы быть правдой .

Преследуя цель - охватить феномен спекулятивных пузырей - мы сфокусируем наше внимание на классе моделей с положительной обратной связью, обсуждавтиихся в главе 4. В данном контексте это означает, что мгновенное приращение цены, как и волатильность, становится больше и больше, когда прошлые цены и/или прошлые приращения и/или прошлые волатильности становятся большими. Как обьясняется в разделе, озаглавленном Интуитивное объяснение возникновения ограниченной по времени сингулярности при tc , ранее в данной главе, положительная обратная связь с увеличивающимся темпом роста также может привести к сингулярности. Здесь это означает, что при отсутствии контроля, цена взлетает вверх без офаничений. Однако наблюдается конкуренция двух эффектов, которые конкурируют, пытаясь вмешаться в это отклонение. Прежде всего, это стохастическая компонента, оказьшающая влияние на изменения цены, делает цену гораздо более беспорядочной, и сходимость к фитической точке становится случайным, неопределенным событием. Это представлено на Рис. 59, иллюсфирующем разнообразие ценовых фаекторий, предшествующих сингулфности B(t).

Рис. 59 показьшает типичную фаекторию пузьфной компоненты цены, сгенерированной моделью с нелинейной положительной обратной связью [396], начиная с некоторой начальной величины вверх вплоть до того времени, когда цены начинают взмьшатъ. Самый простой вариант данной модели состоит из цены пузьфя B(t), являющейся инверсной степенью случайных блужданий W(t), в следующем смысле. Начиная с B(0)=W(0)=0, в начале времени, когда случайные блуждания приближаются к некой величине Wc, которая здесь равна 1, B(t) увеличивается и наоборот. В частности, когда W(t) приближается к 1, B(t) раздувается и достигает сингулфности во время tc, когда случайные блуждания пересекают 1. Данный процесс в случайной области распросфаняет такие сингулфности конечного времени, описанные ранее в данной главе, что монотонно растущий процесс с кульминацией в фитическое время tc заменяется случайными блужданиями, бродящими вверх и вниз, прежде, чем они в конечном счете достигнут фитического уровня. Данный нелинейный положительный раздутый

процесс с обратной связью B(t), таким образом, может бьпъ назван сингулярными обратными случайными блужданиями . При отсутствии краха процесс B(t) может существовать вплоть до конечного времени: с вероятностью 1 (то есть с определенностью), мы знаем из изучения случайных, блужданий, что W(t) в конечном счете достигнет любого уровня, а именно величины Wc=l в нащем примере, при котором B(t) отклоняется.

2500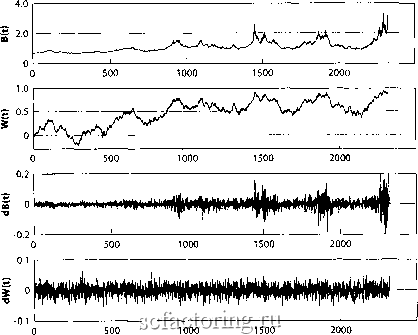

2500

2500

2500

Рис. 59. Верхний фафик: Реализация цены пузыря B(t) в Biv:e функции времени, составленная из сингулярных инверсных случайных блужданий . Это относится к некоторой выборке случайных чисел, используемых при создании случайных блужданий W(t), представленных на втором фафике. Верхняя панель получена путем возведения в степень инверсного значения постоянной Wc, которая здесь она равна 1 минус случайные блуждания, показанные на втором фафике. В данном случае, когда случайные блуждания приближаются к 1, пузырь отклоняется. Обратите внимание на сходность траекторий, показанных на верхнем (B(t)) и втором (W(t)) фафиках, пока случайные блуждания не приближаются к значению Wc=1 слишком сильно. Они могут свободно бродить, но как только они приближаются к 1, цена пузыря B(t) демонстрирует гораздо большую чувствительность и, в конечном счете, опшоняется, когда W(t) доходит до 1. Прежде, чем это произойдет, B(t) может демонстрировать локальные максимумы, то есть локальные пузыри, которые мяп<о сдуваются. Это относится к реализациям того, как случайные блуждания приближаются к Wc, не касаясь его, а затем спонтанно отступают от него. Третий (и, соответственно, четвертый) фафик показывает временной ряд приращений dB(t)=B(t)-B(t-1) пузыря (соответственно, dW(t>iW(t>-W(t-1) для случайных блужданий). Обратите внимание на скачкообразные вспышки сильной изменчивости в пузыре по сравнению с безликим постоянным уровнем колебаний случайных блужданий. Источник [396].

Второе следствие, которое вносит изменения в возможное отклонение цены пузыря, пожалуй, самое важное для режима рьшка с сильно завьштенными ценами. Это воздействие цены на коэффициент угрозы краха, обсуждаемый нами ранее: когда цена взмывает в связи с подражанием, стадностью, спекуляцией и случайностью, коэффициент угрозы краха растет еще быстрее, поэтому произойдет крах и вернет цену назад, ближе к ее фундаментальной величине. Механизмы крахов запускаются сл5Д1айно, управляемые коэффициентом уфозы краха, который является возрастающей функцией пузырной цены. В настоящей формулировке, чем вьпие цена пузыря, тем вьпие вероятность краха. В данной модели крах похож на вьшисанное пациенту слабительное.

Определение коэффициента угрозы краха. Симуляция с использованием компьютерной профаммы идет следующим образом. Во-пфвьтх, мы выбираем дискретизацию времени с шагом St. Затем, зная величину случайных блужданий W(t-dt) и цену B(t-dt) в предшествующее время t-St, мы вьшодим W(t), прибавляя приращение, взятое из цешрированного гауссова распределения с вариацией St. Отсюда мы вьшодим цену B(t), взяв величину, обратную (Wc-W(t)), где а - положительный показатель степени, определенный в модели. Затем мы вьфажаем, при условиях отсутствия арбифажа и рациональных ожиданиях, вероятность h(t) возникновения краха во время следующего временного этапа, где h(t) - коэффициент угрозы краха. Мы фавниваем данную вероятность со случайньм числом гаи, равномфно выбранным в интфвапе [0,1] и запускаем механизм краха, если гаи < h(t). В данном случае цена B(t) меняется на B(t)(l-K), где к взято из предварительно выбранного распределения. Например, спад к при крахе может быть зафиксирован на уровне, скажем, 20%. Слшиком прямолинейно сводить это к арбифажному распределению скачков. После краха динамика продолжается с бесконечно малым приращением, как и раньше, начиная с этого нового значения для времени t, после соответствующего переноса W(t), чтобы обеспечить непрерьшность цен. Если ran > h(t)dt, краха не происходит и динамша повторится на следующем временном шаге.

Таким образом, данная модель предлагает два сценария конца пузыря: спонтатшая дефляция или крах. Эти два механизма являются естественными свойствами модели и не были добавлены искусственно и такие сценарии действительно можно наблюдать на реальных рьшках, что будет описано в гл. 7-9.

Данная модель обладает интересным и далеко идупщм следствием с точки зрения повторения и организации крахов во времени. Действительно, мы видим, что каждый раз, когда случайные блуждания приближаются к выбранной постоянной величине Wc, цена пузьфя взмьшает ввфх, и, согласно условию отсутствия арбитража совместно с рациональными ожиданиями, это подразумевает под собой то, что рьшок входит в опасные воды с приближающимся крахом. Модель случайных блужданий обеспечивает нас очень точньм предсказанием времени ожидания между успетиными приближениями к критическому значению Wc, то есть между успешными пузьфями. Распределение данных сроков ожидания считается очень тиироким степенным распределением [394], настолько широким, что среднее время ожидания является