

 |
 |
|
Факторинг Распределение и корреляция приращений действительных чисел. В то время, как умножение на действительное число соогвегствует сокращению или растяжению вдоль прямой, по контрасту умножение на i соогвеплвуег вращению на прямой угол (равный 90 градусам или я/2 радиан) на плоскости. Умножение на произвольное комплексное число, таким образом, является комбинацией двух преобразований, сжатия или растяжения для действительного числа и вращения (угла, не обязательно равного 90 градусам).  Рис. 77. Геометрическое представление умножения комплексного числа z на другое комплексное число ш: умножение эквивалентно комбинации растяжения и вращения. Оказывается, что введение чисел, подобных i, не приводит к какой-либо непоследовательности и могут применяться все стандартные виды вьршслений. Комплексные числа, будучи чем-то большим, чем чистое творение воображения, сыграли фантастически важную роль для понимания свойств телекоммуникации с помощью электромагнитные и акустических юлн, которыми ежедневно пользуется современная цивилизацщ, поскольку они удобно кодируют двоичную информацию о юлне, а именно ее амплитуду (громкость) и ее частоту и фазу (высоту). Комплексные числа также являются важными элементами простой формулировки одной из самых фундаментальных теорий частиц, в квантовой механике, например, в знаменитом уравнении Шредингера (Schrodinger). Неинтуитивные новейшие явления, описываемые квантоюй механикой, например, такие как принцип суперпозиции, прославившийся в связи с кошкой Шредингера, которая одновременно жива и мертва до тех пор, пока этого никто не наблюдает, технически происходит оттого, что квантовая механика является теорией комплексных чисел. Чтобы бьпъ технически более точным, квантовая механика является теорией их непосредственного (некоммутативного) обобщения, называемого кватернионами. Сейчас мы попытаемся интуитивно объяснить, что комплексные фрактальнью размерности могут привести к логопериодическим осцилляциям, как утверждается вьште. Во-первых, вспомним общий результат, проиллюстрированный Рис. 77, что умножение на комплексное число соответствует комбинации сжатия/растяжения и вращения на плоскости. Для нашей цели давайте забудем о сжатии/растяжении и сосредоточимся только на вращении. Возьмем 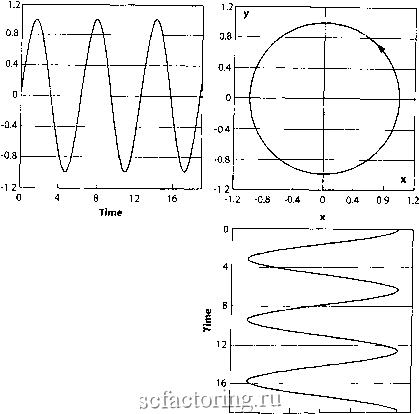 -1.2 -0.8 -0.4 О 0.4 0.8 1.2 Рис. 78. Иллюстрация того факта, что фуговое движение на плоскости х-у соответствует осцилляционным движениям вдоль каждой из координат хи у, соответственно. точку, вращающуюся вокруг центра, как на Рис. 78. Например, рассмотрим верншну секундной стрелки часов, описывающую полный круг в течение тс чно одной мтшуты. Направление вращения для нашего исследования не важно. Эго совершенное периодическое круговое движение на самом деле можно рассматривать как комбинацию двух одновременных и упорядоченных осцилляционных движений, перемещающихся назад и вперед между двумя крайними положениями. Пфвое движение горизонтально и происходит с 9:00 до 3:00, второе движение вертикально и охватывает интервал от 6:00 до 12:00. Рассматриваемое только как проекция на горизонтальную ось, круговое движение вершины секундной стрелки преобразуется в осцилляцию, сходную с осцилляцией на Рис. 78. Это общий результат: любое круговое или локально криволинейное движение может быть преобразовано в комбинацию осцилляционных движений вдоль прямых линий. Возвращаясь к комплексным фрактальным размерностям, нам необходимо дополшггельпо вспомнить интуитивное значение показателя степени. Условные обозначения L=LxLxL и l}=LxL, использованные нами прежде, предполагают, что показатели степени 3 и 2, использованные здесь, указывают, что L умножается па саму себя соответственно 2 и 3 раза. Красота математики часто заключается в обобщении таких очевидньк представлений с целью расширить их использование и подчеркнуть их значение. Здесь обобщение от цельк показателей степени к дробным показателям степени, например, l!, означает, что L умножается на само себя 1,5 раза! Данное любопытное утверждение можно па самом деле сделать точнее, и оно имеет большой смысл. Сходным образом мы можем взять степень комплексного числа с действительным показателем степени: результат показан на Рис. 79. Позволим нашему воображению идти дальше: мы также можем возвести L в степень с комплексным показателем степени. Поскольку, как мы уже сказали, возведение L в какую-то степень соответствует умножению ее на саму себя определенное число раз, здесь мы должны умножить L па саму себя комплексное число раз . Поскольку комплексные числа являются парами чисел, мы вносим смысл в данное любопытное утверждение путем разложения действия комплексного показателя степени на два преофазования, как в случае с умножением. Сконцентрировавшись на вращательном компоненте умножения комплексных чисел, мы можем догадаться (безоишбочно), что комплексный показатель степени L также будет соответствовать вращению. И, наконец, последний этап исследования: поскольку мы рассматриваем действительные числа, такие как цены на фондовом рьшке, это соответствует видению только проекции на действительной прямой комплексного множества операций. Как мы сказали и показали на Рис. 78, вращение проектируется на прямую как осцилляция. Таким образом, построение L, где d является комплексным числом, соответствует проведению осцилляционного логопериодическими осцилляциями Powers of Z умножения. которое оказывается 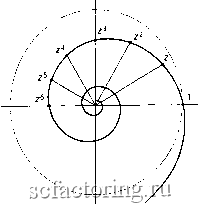 Рис. 79. Геометрическое представление последовательных степеней п=1,2,3... комплексного числа Z для Z внуфи Офужности радиусом 1. Непрерывное изменение показателя степени п как действительного числа дает непрерывную спиралеобразную фивую. Чтобы понять логопфиодическую сфуктуру, нам нужно вспомнить основное свойство логарифмической фушщии, используемой во многих рисунках этой книги, а именно, что логарифм преобразует умножения в перенос, а степень в сложение. Как мы уже сказали, и чем мы уже несколько раз пользовались, логарифмы (с основанием 10) 10, 100, 1000... обозначенные log 10, log 100, log 1000... равны, соответственно, 1, 2, 3... Другими словами, они соответствуют показателю степени 10: 10=10, 100=10 1000=10 Следовательно, осцилляционный вид умножения , индуцированный взятием степени числа с комплексным показателем степени, должен наблюдаться как регулфная осцилляция в логарифме числа, следовательно, как логопериодичность. Мы проиллюсфируем это удивительное явление на Рис. 80 и Рис. 81, показывающих измерение фрактальной размфности в присутствии дисфетной масштабной инвариантности фрактальных объектов. Точнее, мы рассмофим так называемые канторовы множества, которые являются одними из самьтх простых геомсфических объектов, имеющих фрактальные свойства. Рис. 82 показывает первые пять итфаций алгоритма посфоения так называемого троичного капторова множества. На нулевом уровне консфукция канторова множества начинается с единичного интфвала, то есть со всех точек на прямой между О и 1. Этот единичный интервал изображается закрашенным черным цветом офезком на вершине фигуры. Первый уровень получается из нулевого уровня путем удаления всех точек, лежащих в ценфальной фети офезка, то есть всех точек между 1/3 и 2/3. Второй уровень получается из пфвого уровня путем удаления ценфальной фети каждого оставшегося интервала па пфвом уровне, то есть всех точек от 1/9 до 2/9 и от 7/9 до 8/9. В общем, алгоритм посфоепия канторова множества может бьтть описан с:юдующим образом: следующий уровень получается из предьщущего уровня путем удаления ценфальной трети всех интервалов, полученных из предьщущего уровня. Данный алгоритм может бьтть закодирован при помощи следующего символического правила: 1101 и О->000. Этот процесс продолжается до бесконечности, а результатом его является множество точек, которые тонко процежены из единичного интервала. На п-ном уровне множество состоит из N =2 сегментов, каждый из которых имеет тану i =1/3 , так что общая длтша (то есть, измфенпая в математическом смысле) всех сегментов капторова множества равна (2/3) . Данный результат характерен для фрактального множества: так как п сфемится к бесконечности, число деталей (здесь, офезков) экспоненциально растет до бесконечности, в то время как общая длина экспоненциально сфемится к нулю. В пределе бесконечного числа повторений мы обнаруживаем канторово множество, состоящее из бесконечного числа точек нулевого размера. Поскольку каждый раз, когда разрешение увеличивается на множитель 3, появляется в два раза больше Офезков, фрактальная размерность d фоичного множества Кантора является таким, чтобы 2, возведенная в степень d, равнялась 3, отсюда получаем, что d=Ln2/Ln3=0,6309... Канторово множество, являющееся бесконечной пылью точек, представляет собой объект с размерностью, большей чем О (что характфно для точки), по меньшей чем 1 (что характерно для линий). 0.30 I 0.15 О С о и 5-0.15  -0.301- -10 0.30 0.15 3 -0.15 -6 -4 Logj -0.30
-6 -4 Logj Рис. 80. Осцилляционные остатки фрактальных размерностей, полученные из фигуры, показанной на Рис. 82. для (а) троичного канторова (Cantor) множества, посфоенного при помощи итеративного правила 1-+101 и (Ь) Канторова множества, построенного при помощи итеративного правила 1-+1010001. Оба канторова множества имеют одинаковые действительные фрактальные размерности. Они отличаются мнимой частью своих фрактальных размерностей, которая офажается в различных логопериодических структурах, показанных на двух фафиках. Источник [387]. -6 -4 Рис. 81. Степень фрактальной размерности троичного канторова множества, измеренная корреляционным методом. Рисунок изображает логарифм корреляционного интеграла как функцию логарифма размерности. Источник [387]. Различие между результатом измерения фрактальной размерности этого троичного канторова множества и теоретическим значением 0,6309... показана на левом фафике Рис. 80. как функция (логарифмическая ) масштаба. Вместо постоянного значения О, которое получается в случае, если бы фрактальная размфность бьша в точности равной d=Ln2/Ln3=0,6309..., мы, в действительности, наблюдаем сложную осцилляционную сфуктуру вокруг ожидаемого значения, равного 0. Простой результат d=Ln2/Ln3=0,6309... II II 1111 ПИ И II и 11 IIII 1111 1111 IIII Рис. 82. Показывает изначальный единичный интервал и первые пять итераций построения так называемого троичного канторова (Cantor) множества (сверху вниз). Очевидно, что по сфуктуре троичное канторово множество геомефически идентично самому себе только при увеличении с коэффициентом Jijr=3, являющимся произвольными целочисленными степенями 3. Если вы возьмете другой коэффициент увеличения, натфимф, 1.5, то вы не сможете наложить увеличенную часть на изначальное канторово множестю. Таким образом, мы должны заключить, что троичное множество Кантора не обладает сюйстюм непрфывной масштабной инвариантности, но обладает только дискретной масштабной инвариантностью при основном коэффициенте масштабирования 3. Это сюйство проявляется логопфиодическими осцилляциямн. Обратите внимание, что осцилляции сложнее, нежели просто одиночная гладкая синусоидальная структура На самом деле это офажает тфисутствие всех других масштабных коэффициентов 3=9, 3=27..., при которых канторою множество инвариантно. Тонкая сфуктура, видимая на левом фафике Рис. 80, является результатом супфпозиции всех чисто логопфиодических осцилляции, по одному для каждого из допустимых коэффициентов масштабирования. Это похоже на аккорд, составленный путем комбинирования ряда чистых тонов различной громкости. Правый фафик Рис. 80 дает ту же информацию, что и левый для другого канторова множества, полученного по несколько отличающемуся правилу построения: единичный интфвал делится на девять интфвалов длины 1/9 и из них сохраняются только первый, третий, пятый и последний интфвапы. Затем это повторяется с каждым из четырех оставшихся интфвалов. Данное построение символически изображается как правило 1->101010001. Обратите внимание, что каждый раз, когда разрешение увеличивается на множитель 9, появляются четыре новых отрезка. Следовательно, фрактальная размфность d данного ноюго канторова множества должна быть такой, что 9, возведенная в степень d, должна корректно включает в себя часть информации о сфуктуре канторова множества, но, как оказалось, только часть. Как мы объяснили, данные логопфиодические (то есть периодические, в логфифме масштаба £) осцилляции офажают фундаментальную симмефию - дискретную масштабную инвариантность троичного канторова множества. Основной период, видимый на фафике, равен Ln3, что соответствует вьщеленному масштабному коэффициенту 3 дискретной самоподобной консфукции множества Кантора.
|
||||||||||||||||||