Так что же такое фрактал? Всеобъемлющего, окончатель-дого определения фракталов не существует. Мандельброт fl982) первоначально определил фракталы, основываясь на топологической размерности. Впоследствии он отказался от этого определения. Мы будем пользоваться следующим рабочим определением: фрактал есть некоторая самосоотнесенность, или самоподобие. Один из самых наглядных естественных фракталов - это дерево. Древесные ветви следуют фрактальному скейлингу. Каждое ответвление со своими собственными ветвями подобно всему дереву целиком в качественном смысле.

фрактальные формы обнаруживают пространственное самоподобие. Фрактальные временные ряды имеют статистическое самоподобие во времени. Они являются случайными фракталами и имеют больше общего с естественными объектами, чем чистые математические фракталы, которые будут нами рассмотрены в первую очередь. Мы будем изучать в основном фрактальные временные ряды, но фрактальные формы дают хорошую основу для интуитивного постижения, поскольку для них самоподобие имеет наглядный смысл. По аналогии с ними легче будет понять фрактальные временные ряды. Чтобы пробудить читательский интерес, лучше думать о временном ряде рьшочной прибыли. На рис. 5.1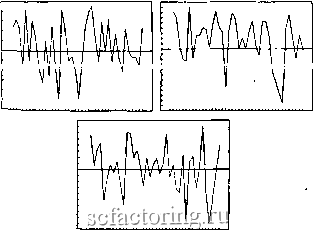

ч меся ° °дабие прибылей, S&P 500: дневные, недельные чные прибыли (можете определить - где какие?).

показаны дневная, недельная и месячная прибыли по статистике S & Р 500 для сорока последовательных наблюдений. Можно ли определить, какой из графиков перед нами, не зная масштабов измерений по осям х и у? Таким образом, рис. 5.1 иллюстрирует самоподобие фрактального временного ряда.

ФРАКТАЛЬНЫЕ ФОРМЫ

Фрактальные формы могут порождаться многими путями. Простейший из них - задать порождающее правило и вьшолнить последовательность итераций. На рис. 5.2 показан пример. Мы начинаем со сплошного равностороннего треугольника (рис. 5.2а). Затем удаляем равносторонний треугольник из первоначальной фигуры - остается три меньших сплошных треугольника и пустой треугольник в середине (рис. 5.26).

Рис. 5.2. Генерация треугольника Серпинского: (а) Начало- Сплошной равносторонний треугольник, (б) Изъятие равносторой него треугольника из центра, (в) Изъятие треугольника из оставшихся треугольников, (г) После 10000 итераций - треугольники внутри треугольников.

Далее удаляются треугольники из этих малых сплошных треугольников (рис. 5.2в). Если мы будем повторять этот процесс, то в итоге получим структуру, показанную на рис. 5.2г - треугольник, который имеет внутри себя бесконечное число уменьшенных треугольников. При увеличении какой-либо части этого треугольника можно было бы увидеть в ней еще больше уменьшенных треугольников. Таким образом, бесконечное число треугольников заключено в конечном пространстве исходного треугольника. При помощи простого правила в этом конечном пространстве создана бесконечная сложность. Этот особенный фрактал, называемый треугольником Серпинского, как мы увидим дальше, играет определенную роль в анализе временных рядов.

Теперь попытаемся применить к треугольнику Серпинского евклидову геометрию. Он не одномерный, так как не является линией. И не двумерный, как сплошной треугольник, ибо имеет в себе отверстия. Его размерность заключена между единицей и двойкой. Она равна 1.58 - это дробная, или фрактальная, размерность. Фрактальные размерности являются главными идентификационными характеристиками фракталов. Проницательную мысль Мандельброта о том, что фрактальная размерность существует естественным образом, можно сравнить с изобретением числа (0) (нуль) средневековыми восточными математиками, или с изобретением отрицательных чисел раннеиндийскими математиками. Фрактальные размерности - объективная реальность. Прежде не привлекавшие внимания, теперь они углубили и расширили дескриптивную мощь математики.

склонны лумнть. чт някий плоский o6i.cKT является двумерным. С точки зрения математики это не так. Евклидова плоскость есть ровная поверхность без щелей и проломов.

одобным же образом мы склонны считать, что объект, имеющий глубину - является трехмерным. И снова, в евклидовой геометрии это не так. Трехмерный объект есть чистая лошная форма. Математически он отличается свойством оеи полной поверхности. Он не имеет в ней дыр и щелей. ледовательно, объект, обладающий глубиной, не обязатель-является трехмерным. Например, фиксирующий шарнир кли*- собой шар с углублениями; в соответствии с ев-ер геометрией он не является трехмерным, поскольку

Поверхность не гладкая.