

 |
 |
|
Факторинг Рынок капитала Обратимся к рассмотрению временного ряда фондовых цен, который представляет собой зазубренную линию. Она не одномерна, потому что не есть прямая. Но она также и не двумерна, поскольку не заполняет плоскость. На языке размерностей она более чем линия и менее чем плоскость. Ее размерность находится между единицей и двойкой. (В главе 9 мы установим, что эта кривая статистики S & Р 500 имеет размерность 1.24) Другой пример фрактальной формы - снежинка Кох. Подобно треугольнику Серпинского, снежинка Кох создается ад- 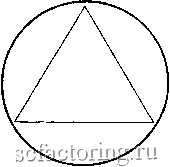 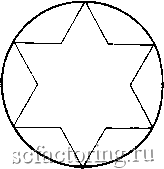 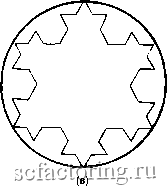 Рис. 5.3. Генерация снежинки Кох. (а) Начало - равностороннй треугольник, (б) Добавление равностороннего треугольника на ной третьей части каждой из сторон, (в) Продолжение процеДУР добавления треугольников. Случайные фракталы 73 дитивным правилом. На рис. 5.3 показана эта процедура. Она начинается с равностороннего треугольника (рис. 5.3а). На средней трети каждой из сторон строится другой равносторонний треугольник, образуя форму, показанную на рис. 5.36. При повторении шага б получим в результате снежинку (рис. 5.3в). Такая снежинка, в принципе, имеет бесконечную длину, поскольку треугольники могут добавляться до бесконечности. Однако окружность, которая заключает в себе исходный треугольник, ограничивает это пространство. Мы имеем бесконечную длину внутри конечного пространства. И чем ближе мы будем рассматривать профиль этой снежинки, тем больше деталей увидим. Будут видны уменьшенные версии большой формы. Путем простого итеративного правила снова создан объект бесконечной сложности, заключенный внутри конечного пространства. Два этих примера-треугольник Серпинского и снежинка Кох - являются симметричными фракталами. Они часто называются детерминистическими фракталами, потому что создаются с помощью детерминистических правил. Как мы установили, естественные объекты в действительности никогда не бывают симметричными. Две рассмотренные фрактальные формы, следовательно, не представляют природные формы или рынки капитала, однако они иллюстрируют некоторые важные характеристики фракталов. Они являются объектами, созданными посредством простых итерационных правил, дающих самоподобные формы с фрактальными размерностями. Более реалистичными являются случайные фракталы. СЛУЧАЙНЫЕ ФРАКТАЛЫ Хорошим примером случайных фракталов могут служить береговые линии. С самолета на большой высоте береговая линия выглядит гладкой нерегулярной кривой. При уменьше- и высоты полета выявляется зазубренность береговой ли-J наконец, при ближайшем рассмотрении виден каждый Чайший выступ. Кривая цен на фондовом рынке сравни-изм* Рвыми линиями. Эта зазубренная линия, ценовых инияч прибылей, сначала выглядит как береговая Мер ближе мы рассматриваем временной ряд (напри-Аетале временной интервал на рис. 5.1), тем больше Случайные фракталы представляют собой комбинации порождающих правил, выбранных наугад в разных масштабах. Можно привести в качестве примера структуру легкого млекопитающих. Наше легкое имеет главный стебель, трахею, которая в свою очередь имеет два первых ответвления. Эти две ветви имеют еще больше ответвлений. Диаметры этих ответвлений уменьшаются, в среднем, в соответствии с показательным законом. Этот скейлинг является фрактальным. Однако легкое - не симметричный фрактал, подобный снежинке Кох. Каждое поколение имеет, в среднем, уменьшенный диаметр, но отдельные ветви могут варьироваться в размерах. Скейлинг каждого нового поколения не имеет какого-то характеристического масштабного коэффициента. Это - естественное правило , которое является причиной множественного скейлинга, связанного с аддитивным процессом данной системы. Если диаметр одной части ветвящегося поколения уменьшается, то это компенсируется другой его частью. Естественная селекция работает в пользу случайного фрактального скейлинга, хотя и она также случайна. Такая комбинация случайности и детерминированности, порождая правило, или причинность , может быть также полезной в анализе рынков капитала. ИГРА ХАОСА Майкл Барнсли (Michael Bransley) из фирмы Itereted Systems, Inc., разработал математический аппарат для порождения фрактальных форм, который назвал итеративными функцио-на..пьными системами CTterated Fnnction Systems - IFSl. В одном из подмножеств IFS фракталы порождаются детерминистическим правилом, которое выполняется случайным образом. В результате появляется нечто такое, что трудно даже себе вообразить. Барнсли назвал свой алгоритм игра хаоса. Одна из форм игры хаоса показана на рис. 5.4. Начинается игра с трех равноотстоящих точек (рис. 5.4а). Пометим точку А как (1,2), точку В как (3,4) и точку С как (5,6). Это игровая доска. Выберем теперь некоторую точку внутри треугольника ABC. Чтобы сыграть в эту игру, бросаем игральную кость (убедитесь, что кость имеет правильную форму). Продвинемся на половину пути до точки, номер которой выпал. Например если выпало 5, пройдем половину отрезка до точки G
|