Если в двойных логарифмических координатах найти наклон R/S как функцию от N, то тем самым мы получим оценку Я. Эта оценка не связана с какими-либо предположениями относительно лежащего в основе распределения.

Для очень большого количества наблюдений N можно ожидать сходимости ряда к величине Я = 0.50, так как эффект памяти уменьщается до того уровня, когда становится незаметным. Другими словами, в случае длинного ряда наблюдений можно ожидать, что его свойства станут неотличимы от свойств обычного броуновского движения, или простого случайного блуждания, поскольку эффект памяти рассеивается. Регрессия в этом случае должна выполняться до того как Я приблизится к 0.5, так как корреляционная мера (7.4) не применима ко всем без исключения приращениям.

Важно напомнить, что корреляционная мера (7.4) пе имеет отношения к автокорреляционной функции гауссовских случайных переменных. Последняя предполагает гауссовские или почти гауссовские свойства лежащего в основе распределения-хорошо знакомую красивую кривую. Автокорреляционная функция хорошо работает в определенных краткосрочных зависимостях, однако имеет тенденцию преуменьшать долгосрочные корреляции в негауссовских рядах. Читателям, интересующимся полным математическим объяснением того, почему авгокорреляциопп;1л функция if даст хороших зультатов в процессах с долговременной памятью, рекомендуем обратиться к статье Мандельброта (1972).

На рис, 7.3 в двойных логарифмических координатах представлена кривая зависимости R/S от N для Я = 0.5, построенная по данным из рис. 7.1. Эти данные были получены с помощью генератора псевдослучайных чисел с гауссовскиМ выходом и показывают Я = 0.55 ±0.1. Эта оценка немного выше, чем ожидалось, но эти псевдослучайные числа сгенерированы детерминистическим алгоритмом. Это может быть причиной смещения. Важно заметить, что Я/5-анализ - этО исключительно устойчивый метод. В его основе нет предположения о гауссовском распределении. Найденное значение Я = 0.50 не является доказательством того, что налицо глус

ОЦЕНКА ПОКАЗАТЕЛЯ ХЕРСТА

Прологарифмируем соотношение (7.3):

log{R/S) = Я * (log(iV) + log(a)). (7.5)

Оценка показателя Херста 97

0.4 О.б О.в t 1.2 1.4 t.6 1.8 2 2.2 2.4 2.е

1од(количество наблюдений)

Рис. 7.3. Д/5-анализ: случайные гауссовские числа. Фактическое значение Я = 0.5, оценка Н = 0.55.

совское случайное блуждание, оно доказывает только то, что это процесс, который отличается короткой памятью. Другими словами, любая независимая система, гауссовская или какая-либо другая, может продуцировать Я = 0.5.

На рис. 7.4 показана аналогичная кривая для Я = 0.72 - значения, часто наблюдаемого в природных процессах. Эти даннмр (пни т.акжс предст.авлепы па рис. 7.1) были п.олучгпы аппроксимацией обобщенного броуновского движения, более детально описанной в Приложении 3. Такой ряд получен, как было сказано, с учетом памяти о 200 наблюдениях. В имитаторе Херста, использующем смещенную колоду из 27 карт, эффект памяти моделировался джокером. Он мог появляться, в Среднем, после 27 снятий колоды, в продолжение большого количества имитаций. Имитатор Херста располагал памятью о 27 наблюдениях. Долгосрочные корреляции после 27 наблюдений падают до нуля, и при шаге по времени 27 наблюдений Или более система начинает следовать случайным блуждани- Таким образом, мы могли бы принять эти 27 наблюдений как цикл, или период, системы. Данные, которые были зяты для построения кривых на рис. 7.1 и 7.2, имитируют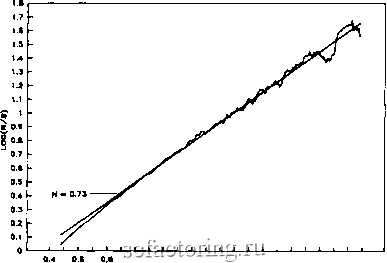

I 1.2 1.4 1.6 .в 2

1од(количество наблюдений)

2.2 2.4

Рис. 7.4. анализ: фрактальное броуновское движение. Факт]

ческое Н = 0.72, оценка Я = 0.73.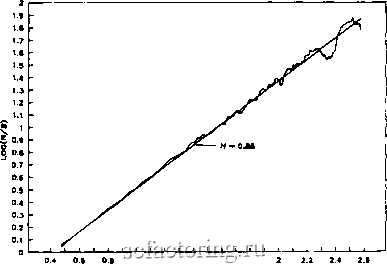

I 1.2 1.4 1.6 1.8

1-од(количество наблюдений)

Рис. 7.5. Д/5-анализ: фрактальное броуновское движение. Фактическое Я = 0.90, оценка Я = 0.86.