не быть таковыми, если существуют краткосрочные зависи-j мости марковского типа, простирающиеся дольше шести ме сяцев. Эту ситуацию мы обсудим позже.) Теперь мы можел применить уравнения (7.1) и (7.2) и подсчитать размахи nd каждому шестимесячному периоду. Пронормируем их соот-1 ветствующими стандартными отклонениями, чтобы получит!] 80 отдельных Д/5-наблюдений. Посредством осреднения эт1 наблюдений мы получим оценку R/S для N = Q месяцам.

Продолжим подсчет для N = 7, 8,9,... , 240. При это\ можно ожидать уменьшения устойчивости в оценке R/S, та как уменьшается количество осредняемых наблюдений. Сс вокупность расчетов для всего диапазона N дает регрессии log{R/S) на \og{N), и, в соответствии с уравнением (7.3), на клон линии регрессии даст оценку для Н. Однако же оцени-! вать Н для полного диапазона N было бы неправильным вви ду того, что ряд имеет конечную память и начинает следоват случайным блужданиям. Теоретически процесс с долговре менной памятью предполагается берущим начало из бесконеч но удаленного прошлого. Но в дальнейшем, при рассмотрении теории хаоса, мы увидим, что в любой нелинейной системе, ее движении, всегда существует точка, где теряется память начальных условиях. Эта точка потери аналогична конг естественного периода системы. Чтобы убедиться в том, дт,ей- ствительно ли имеет место подобный переход, следует вни4 мательно изучить данные. Регрессия, возникающая в конц определенного диапазона данных, может свидетельствоват о процессе с долговременной памятью. Другой путь pemenni этой проблемы связан с открытием фрактального скейлиг гя в лрутих природных системах. Теоретически все фракталы имеют бесконечную масштабную инвариантность, подобно треугольнику Серпинского. Однако естественные фракталы, такие, как например сосудистая система человека, не таковы-Физиологи установили, что изменения в диаметрах артерий и вен следуют фрактальному скейлингу в своих разветвлениях. Эта фрактальная система имеет предел, так как сосудистая система не становится бесконечно малой - диаметр сосудов остается конечной величиной. Аналогично этому я предполагаю, что процессы с долговременной памятью в большинстве систем не бесконечны - они имеют предел. Сколь долга эта память, зависит от структуры нелинейной динамической системы, которая порождает фрактальный временной ряд. По

той причине визуальная оценка данных по двойной логариф-1Ической кривой перед измерением Н очень важна.

Теперь встает вопрос в отношении данных: как много их должно быть? Федер говорит, что имитация с количеством на-людений менее 2500 может быть поставлена под вопрос, но :ри этом не указывгьет - сколько должно быть эксперимен-альных точек для адекватной оценки. В физических науках :сследователи могут получать тысячи экспериментальных то-ек при контролируемых условиях. В экономической теории, виду того что мы ограничены относительно короткими ря-;ами, которые при том заключают в себе разнообразные вли-ния рыночной среды, мы должны быть очень внимательны своем анализе.

Я считаю, что мы имеем достаточно данных, когда есте-твенный период системы может быть легко различим. Тогда нашем распоряжении имеются различные циклы данных, рступные для анализа, и это количество должно быть до-таточным. В дополнение к этому теория хаоса утверждает, то достаточно данных десяти циклов. Если мы можем оце-ить длину цикла, то тогда соответственно использовать 10-цкловый общий курс как совокупность адекватных данных.

В этом главе мы будем в основном анализировать месяч-ые данные из различных доступных источников, начиная с 920-х годов. В следующей главе изучению будет подвергнут сказатель Херста Н относительно его поведения при различ-ых приращениях прибыли - от одного до девяноста дней.

ФОНДОВЫЙ РЫНОК

Начнем с применения Д/б-анализа к месячным.данным рей-инговой компании Стандард энд Пур (S&P 500) за 38-летний ериод с января 1950 по июль 1988 гг. На рис. 8.1 показана Ривая в двойной логарифмической шкале, полученная опи-э-нным выше методом. Процесс с долговременной памятью людается приблизительно в продолжение 48 месяцев. По-этой точки график начинает следовать случайным блужданиям при Н = 0.50. Прибыли, которые отстоят др.уг от Руга более чем на 48 месяцев, имеют в среднем малую ле- стороннюю корреляцию. На рис. 8.2 представлены вели- пы я, рассчитанные по регрессиям для N, меньших или вных 3, 3.5, 4, 4.5 и 5 годам. Пик явно наблюдается при 4 годам с Н = 0.78, и мы можем сказать, что это оценка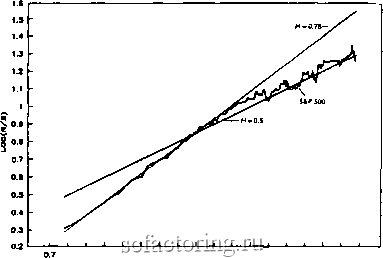

1.1 1.3 1.S 1.7 1.9

иод(количество месяцев)

Рис. 8.1. Д/5-анализ; месячные прибыли, S&P 500, январь 1950-июль 1988 гг. Оценка Н = 0.78 (с разрешения Financia Analysti Journal).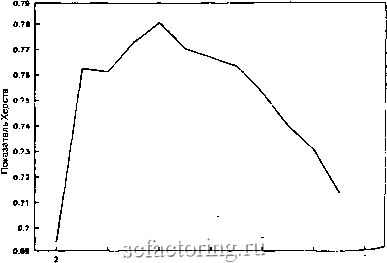

N <= количества лет

Рис. 8.2. Д/5-анализ: оценка длины цикла, S&P 500, месячные пр были, январь 1950 -- июль 1988 гг.