Глава 10

Фракталы и хаос

Мы установили, что фракталы порождаются нелинейными динамическими системами, однако не обсудили, что это означает. В этой главе мы установим интуитивную связь между этими двумя концепциями, что естественным образом приведет к проблематике части 3. Речь пойдет главным образом о логистическом уравнении - математической модели, которая уже была затронута в гл. 1. Логистическое уравнение - это простая одномерная модель, которая демонстрирует богатство хаотического поведения, включая переходы от порядка к хаосу в определенной последовательности. Это уравнение исследовал Мэй (May, 1976), а Фейгенбаум (Feigenbaum, 1983) нашел новую универсальную константу, встроенную в его систему. В дополнение ко всему изображение его возможных решений образует статистическую структуру, в которой легко увидеть фрактал. Поэтому данная глава будет касаться больше этой математической модели, нежели финансовых инвестиций и экономической теории. Как и в других разделах книги, изложение ведется на интуитивном уровне. Тех, кто заинтересован в более строгом математическом изложении, мы отсылаем к статьям Мэя и Фейгенбаума, а также к учебнику Девани (Devaney, 1989).

ЛОГИСТИЧЕСКОЕ УРАВНЕНИЕ

Как было показано в гл. 1, обш,ей формой логистического уравнения является:

Xt+i = 4:*a*xt*{l - xt), (10-1)

где О < < 1, О < а < 1.

Логистическое уравнение представляет собой одномерную Нелинейную систему с обратной связью. Оно является также разностным уравнением, в противоположность непрерывной -истеме, такой, как получается из дифференциальных уравне-

НИИ с частными производными. Следовательно, это дискретная Система. Как разностное уравнение оно легко может быть исследовано в электронной таблице путем следующей процедуры:

1. В ячейку А1 поместить начальное значение константы о между О и 1. Начать с 0.50.

2. В ячейку В1 поместить начальное значение х = 0.1.

3. В ячейку В2 поместить формулу:

4*$Л$1*В1*(1-В1).

Заметим, что значение о в ячейке Al остается постоянным.

4. Скопировать ячейку В2 вниз по крайней мере на 100 ячеек.

Посредством построения графика по данным колонки В как временного ряда мы можем изучить переход системы от устойчивости к хаосу.

ПУТЬ к ХАОСУ

Рассматривая временные ряды с о = 0.5, мы можем увидеть, что после начального всплеска система устанавливается на одной устойчивой величине (рис. 10.1). Увеличение о до 0.6 снова демонстрирует сходимость ряда, однако на величине несколько большей.

Количество итераций

Рис. 10.1. Логистическое уравнение; сходимость x{t); а = 0.50.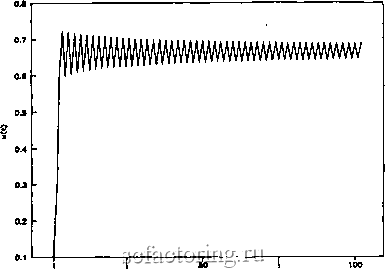

2В 7S

Количество итераций

Рис. 10.2. Логистическое уравнение: а = 0.75, два периодических решения.

Увеличение а не дает ничего интересного до тех пор, пока мы не достигнем а = 0.75. Неожиданно система перестает устанавливаться на одной величине, а начинает осциллировать между двумя величинами (рис. 10.2). Это расщепление, переход от одного к двум потенциальным решениям называется бифупкяттирй

Если продолжить увеличение а, то приблизительно около 0.87 (точнее -0.86237...) система вновь теряет устойчивость и появляются четыре возможных решения, как это показано на рис. 10.3. При дальнейшем увеличении а система будет вновь и вновь терять устойчивость. Критические величины а Возникают все чаще и чаще и располагаются все ближе друг к другу. При а = 0.886 мы получаем восемь решений, при ° = 0.8911 - шестнадцать, при о = 0.8922 - тридцать два, при °- = 0.892405 - шестьдесят четыре решения. Это увеличение Продолжается до а = 0.90 (точное значение - 0.892486418). Десь происходит нечто удивительное.

При а = 0.90 система полностью теряет устойчивость. Чис- о решений становится бесконечным. При взгляде на времен-