

 |
 |
|
Факторинг Рынок капитала 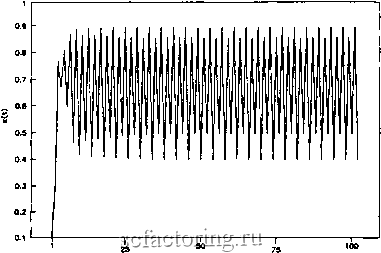 Количество итераций Рис. 10.3. Логистическое уравнение: сходимость x{t); а = 0.87. Че- тыре периодических решения, или четыре возможных конечны: величины. 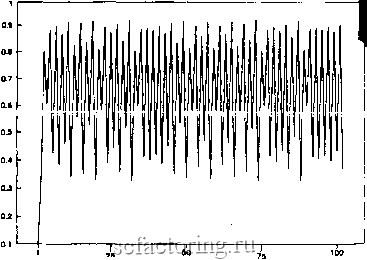 Количество итераций Рис. 10.4. Логистическое уравнение: сходимость x{t); а = 0.90-Хаотическое поведение, или бесконечное количество возможных величин. Рождение и смерть 151 ной ряд на рис. 10.4 мы видим хаос. Ряд выглядит случайным, и, если подвергнуть его статистическому анализу, то он таковым и окажется. Действительно, логистическое уравнение используется как датчик случайных чисел. Примером физической системы, которая ведет себя подобно логистическому уравнению, является громкое вещание. Если микрофон воспринимает негромкую речь, можно услышать басовитое гудение. Если же громкость речи увеличивается, то в громкоговорителе внезапно начинают сменяться два фоновых тона. При дальнейшем увеличении громкости возникает еще больше бифуркащ1й, и на критическом уровне неуправляемая обратная связь приводит систему к аудиохаосу. Это простое уравнение демонстрирует очень сложное поведение. Больше того, детерминистическое уравнение дает нам пример хаоса. Рассмотрим же его более внимательно. РОЖДЕНИЕ И СМЕРТЬ Логистическое уравнение первоначально было использовано для моделирования популяционной динамики в экологии. В экологических популящюнных системах имеют место скорость рождений и скорость умираний. Модель роста популяции будет простым нелинейным уравнением: xt+i = а* xt. (10-2) В такой системе популяция растет бесконечно и неуправляемо со скоростью а * X. Чем больше растет популяция, тем меньше ресурсов становится для ее поддержания. В систему Необходимо ввести скорость умирания. В логистическое уравнение добавляется скорость умирания в виде а* х. Вычитая Эту величину, мы получаем из (10.2) логистическое уравнение (10.1). Его решение растет как о * ж, но ограничивается 1леном о * х. Если константа о увеличивается, то механизм Нелинейной обратной связи приводит к тому, что популяция может находиться более чем в одном устойчивом состоянии. Вследствие этого при достижении нижнего предела величины Популяция снова начинает располагать ресурсами для роста н достижения большего размера. Эта взаимосвязь становится более сложной при увеличении о. ФРАКТАЛЬНАЯ ПРИРОДА ЛОГИСТИЧЕСКОГО УРАВНЕНИЯ Формально не существует математической связи между хаотическими системами и фракталами. Тем не менее ее легко прпг.тгдитт, ТТЛ гр.афико гозлтожных рртттений vaoTK4PCKOH системы. Даже одномерная система, подобная логистическому уравнению, демонстрирует свою фрактальность. На рис. 10.5 представлена бифуркационная диаграмма логистического уравнения. На график нанесены возможные величины X, соответствующие различным константам а. (Краткое описание бейсик-программы, выполняющей вычисления и рисование графика, дано в Приложении 1.) Из графика видно, что несмотря на хаотичность системы, имеет место определенная упорядоченность в ее возможных решениях. На нижнйХ уровнях а существуют единичные равновесные решения. Видны также точки бифуркаций и область хаоса между значениями а, равными 0.90 и 1.0. Но даже в хаотической области наблюдается некий порядок. УПОРЯДОЧЕННЫЙ БЕСПОРЯДОК Выше мы заметили, что критические точки, где имеют место бифуркации, становятся все ближе друг к другу, по мере того как величина а растет. Фейгенбаум (1983) показал, что это случается с определенной последовательностью. Он также высказал догадку, а Лэнфорд (Lanford, 1982) доказал, что эта последовательность постоянна и универсальна для всех параболических нелинейных систем. Ее постоянство позволяет предсказывать появление следующего критического уровня а. Следовательно, мы можем классифицировать различные хаотические функции. Фейгенбаум нашел следующую закономерность в чередовании бифуркаций: (Ьп ~ bn-i) 4 669201609... , [Оп+Х - On) где Ь -значение а при п-ой бифуркации. Величина 4.6692 называется числом Фейгенбаума и обозначается через F. Оно является новой универсальной постоянной, подобно числу 7Г или основанию натуральных логарифмов е.
|