-0.1 0.1 ОЛ Текущий момент

Рис, 13,36. Двумерный фазовый портрет индекса MSCI немецких обыкновенных акций. Логарифмически-линейное детрендирование, январь 1959 -февраль 1990 гг.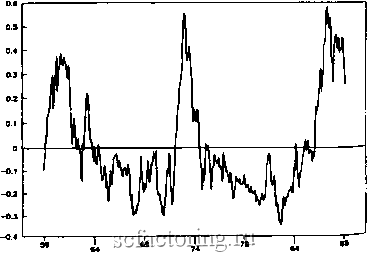

Годы

Рис. 13.4а. Временной ряд индекса MSCI японских обыкновенных акций. Логарифмически-линейное детрендирование, январь 1959 февраль 1990 гг.

-0.4

Н>.4 -ОЛ О ОЛ

Текущий момент

Рис. 13.46. Двумерный фазовый портрет индекса MSCI японских обыкновенных акций. Логарифмически-линейное детрендирование, январь 1959 -февраль 1990 гг.

следующих резких падений со стабилизацией состояния. Такая картина наблюдалась в конце 50-х, конце 60-х и с середины до конца 80-х годов. Подобным образом в 1990 г. фаза гиперроста снова продемонстрировала самокоррекцию.

Эти восстановленные фазовые пространства не являются хгиггсскими-/ графика.ми, и11101.ящимио1 к гехиическиму анализу (точки, диаграммы и т. п.). Они являются базовыми данными для нахождения характеристик, необходимых для определения рынков как нелинейных динамических систем.

можем использовать теперь эти детрендированные дан-bie для восстановления фазовых пространств, расчета фрак-ьных размерностей и показателей Ляпунова.

ФРАКТАЛЬНЫЕ РАЗМЕРНОСТИ

рассчитываем фрактальную размерность способом, изло-Днным в гл. 12. Во-первых, в соответствии с уравнением 2) рассчитываются корреляционные интегралы для по-Довательного увеличивающихся размерностей вложения.

а: о

-г.*

-1.

-1.2 -ОЛ -О.*

loo(R)

Рис. 13.5. Корреляционные интегралы: индекс S&P 500, детрендй-рованный индексом CPI (воспроизведено с разрешения Financial Analysts Journal).

При этом просматриваются регрессии на линейных областях двойных логарифмических кривых. Фрактальная размерность должна в конце концов сходиться к своей истинной величине, по мере того как будет увеличиваться размерность вложения.

На рис. 13.5-13.8 показаны диаграммы корреляционных интегралов для четырех рынков. Линейные области на каждой диаграмме могут быть использованы для построения регрессий. На рис. 13.9-13.12 показана сходимость к фрактальной размерности. В табл. 13.1 дана сводка результатов.

США, Англия и Германия имеют фрактальную размерность между 2 и 3. Это хорошая новость, потому что это означает, что есть возможность смоделировать динамику этих рынков с помощью трех переменных. Мы не знаем, каковы эти три переменные, но графическое изображение трех переменных представляет собой решаемую проблему.

Для Японии мы видим другую картину. Ее фрактальная размерность равна 3.05, и это означает, что необходимы четыре переменные. Японский рынок более сложен, чем три других рассмотренных рынка.