Нечеткие множества

Как мы установили, нечеткое множество является способом описания сложных понятий. Чем больше становится их сложность, тем более нечеткими становятся сами понятия. Например, множество целых чисел от 1 до 10 есть простое четкое множество. Однако предположим, чтв-множество составляют целые числа около шести . Пять около шести. Так же и семь, и восемь. Но что сказать относительно 11 или 16? Нечеткие множества дают нам точный способ определения этого понятия- около 6 , но он субъективен. Графически это можно представить так, как сделано на рис. 15.1.

1.0 0.8 О.б 0.4 0.2 0.0

1 2 3 4 5 6 7 8 9 10 11 12

Рис. 15.1. Четкое множество: числа около 6 .

дробные величины этого промежутка. Так, человек шести фу. тов роста имеет функцию принадлежности, равную единице в множестве высоких людей, в то время как некто пяти футов одиннадцати дюймов может иметь функцию принадлежности 0.9, а некто пяти футов четырех дюймов -- функцию принадлежности 0.1. Теория множеств была обобщена, и внезапно исчезли все парадоксы. Теперь мы можем строго определить туманные понятия, такие, как например куча . Груда в 1000 песчинок имеет функцию принадлежности 1.0 к множеству куча . Груда в 20 песчинок имеет функцию принадлежности 0.4. Как это было в случае с фракталами, обобщение теории с включением дробных величин размерности увеличивает ее полезность и укрепляет связи с реальностью.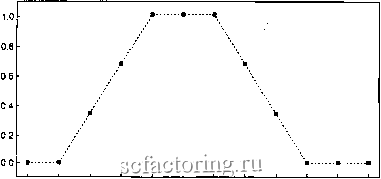

1 2 3 4 5 6 7 8 9 10 11 12

Рис. 15.2. Функция нечеткой принадлежности; числа около 6 .

В четком множестве мы должны были бы решить точно, что означает около 6 . Если мы решим, что числа от 5 до 7- около 6 , мы получим рис. 15.2. На нем показано подобие чисел понятию около 6 . По оси у располагаются функции принадлежности. Как можно видеть, в терминах обычного четкого множества величины, меньшие 5 или большие 7 получают величину функции принадлежности, равную 0. Они не около 6 . Только числа 5, 6 и 7- около 6 , и, будучи таковыми, они все равны между собой. В нечетком множестве мы должны решить вопрос относительно того, являются ли числа определенно не около 6 и каковы функции принадлежности каждого числа. В данном примере мы установим, что число, меньшее 2 или большее 10, - определенно не около 6. Величины от 5 до 7 - определенно около 6 и, следовательно, имеют функцию принадлежности, равную 1. В диапазоне От 2 до 5 проводим прямую линию от у = О до у = 1. От 7 ДО 10 также проводим прямую с отрицательным наклоном от У = 1 до у = 0. Величины ординат этих прямых соответствуют функциям принадлежности чисел, расположенных по оси абсцисс, к множеству числа около 6 . Таким образом, число 4 имеет величину функции принадлежности 0.67, а число 5 - Величину функции принадлежности 1. Пять в большей степени около 6 , чем 4, но 4 остается около 6 . Мы могли бы Получить границы множества, подобные форме функции принадлежности, различными способами. Как мы делаем выбор? От в чем состоит сила и слабость нечетких множеств. Пара- етры такого выбора субъективно зависят от природы про-

0.8 0.6 0.4 h 0.2 0.0

-I-1 ...il-1-, 1 I -i.. I I-1, I 1. -L- ----

1 2 3 4 5 6 7 8 9 10 11 12

Рис. 15.3. Нечеткое дополнение: числа около 6 .

блемы. Адекватность модели зависит от того, как хорошо создатель модели понимает проблему. Хорошее понимание проблемы даст в результате хорошую нечеткую модель. Однако модель, разработанная при ошибочном понимании проблемы даст результаты со всеми теми ограничениями и ошибками, которые может сделать моделирующий.

Кроме того, существуют различные определения для дополнения, объединения и пересечения нечетких множеств. Они подобны правилам для четких множеств. Мы дадим здесь основные определения; обобщенные определения могут быть изучены более подробно по книге Заде и Каспржик (Zadeh, Kacprzyk, 1992):

А - принадлежность множеству Л, 0<Л<1 (15.1)

1 - Л -дополнение множества А (15.2)

Min(A, В) - пересечение множеств А и В (15.3)

Мах{А,В) - объединение множеств Ал В (15-4)

Как можно видеть, дополнение нечеткого множества есть единица минус функция принадлежности. Так, если 4 на 0.67 принадлежит множеству около 6, оно также на 0.33 не принадлежит множеству окшю 6. Закон исключенного третьего был одним из первых среди причин перехода к теории нечетких множеств. В нечетких множествах объект может принадлежать как множеству, так и его дополнению. Это может быть прослежено графически на рис. 15.3.

Неч *тков множество Нечеткое дополнение j

1.01-♦..............♦. *....... .......щ ♦