

 |
 |
|
Факторинг Управлению капиталом Тут читатель может возразить, что мы не собираемся без конца повторять эту сделку, мы проводим ее лишь однажды. Мы не реинвестируем вновь в одни и те же сценарии. Разве не лучше всегда выбирать сценарий с наибольшим математическим ожиданием для каждого набора решений, с которым мы сталкиваемся? Ориентироваться на максимальное арифметическое математическое ожидание нужно лишь тогда, когда вы намерены сделать последнюю ставку и прекратить игру. Однако почти всегда мы продолжаем ее, и деньги, которыми мы рискуем сегодня, завтра же снова будут поставлены на кон. При этом предьщущие выигрыши и проигрыши влияют на то, чем мы в состоянии рискнуть сегодня. В этой ситуации мы заинтересованы в максимальном росте нашего капитала в долгосрочной перспективе и нам следует ориентироваться на большее среднее геометрическое. Даже если сценарии, которые появятся завтра, будут отличаться от сегодняшних, мы все равно максимизируем эффективность наших решений, если всегда будем отдавать предпочтение большему среднему геометрическому. То же самое происходит при выборке без замещения или при игре в очко. От сдачи к сдаче вероятности меняются, как меняется и оптимальная доля счета, которую следует ставить на кон. Однако, постоянно ставя на следующий кон оптимальную долю для текущей сдачи, мы максимизируем наш долгосрочный рост. Помните, что для максимизации долгосрочного роста мы должны исходить из того, что текущий расклад будет бесконечно повторяться в будущем. Другими словами, мы должны рассматривать каждое отдельное событие, как если бы мы ставили на него бесконечное количество раз, если хотим максимизировать рост за много розыгрышей с различными раскладами. Обобщая, можно утверждать, что если исход события влияет на исход(-ы) следующего события(-ий), то нам лучше предпочесть решение с наибольшим геометрическим ожиданием. В редких случаях, когда исход события не влияет на последующие события, лучше ориентироваться на наибольшее арифметическое ожидание. Математическое ожидание (арифметическое) не учитывает дисперсии исходов различных сценариев и поэтому может привести к неверным решениям в контексте реинвестирования. Использование данного подхода к сценарному планированию позволяет выбирать размер позиции, исходя из возможных сценариев, их исходов и вероятностей реализации. Этот подход внутренне более консервативен, чем ориентация на наибольшее математическое ожидание. Среднее геометрическое набора чисел не превосходит их среднего арифметического. Поэтому наш подход никогда не перегрузит (в смысле размера позиции) вас так, как это бывает при ориетации на максимальное математическое ожидание. В ассимптотическом смысле (в долгосрочной перспективе) превосходство данного метода проявляется не только в том, что он позволяет вам достичь наибольшего геометрического роста, но также и в большей его консервативности по сравнению с ориентацией на критерий наибольшего математического ожидания. Поскольку реинвестирование стало чуть ли не каждодневным (за исключением дня, предшествующего уходу от дел), текущие решения нужно принимать, исходя из того, что они будут задействоваться тысячи раз, и таким образом максимизировать их совокупную эффективность. Мы должны принимать свои решения и инвестировать так, чтобы максимизировать геометрическое ожидание. Далее, поскольку исходы большинства событий действительно влияют на исходы последующих событий, мы должны действовать, ориентируясь на максимум геометрического ожидания, что может привести к инвестициям, которые не всегда очевидны. Сценарные спектры Теперь мы должны подробнее остановиться на понятии сценарного спектра. Сценарный спектр - это набор сценариев с вероятностями от О до 1, упорядоченных от наихудшего исхода к наилучшему. К примеру, сценарный спектр простой игры в монетку, где мы с равной вероятностью проигрываем на орлах И выигрываем на решках, состоит из двух сценариев, каждый из которых реализуется с вероятностью 0,5 (рис. 1.7). Сценарный спектр может содержать более двух сценариев -столько, сколько вам угодно (рис. 1.8). Probabilities Worst case 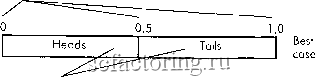 Scenarios Рис. 1.7. Probabilities Worst case
Best cose Scenarios Рис. 1.8. Этот сценарный спектр соответствуют сценариям из предыдущего раздела, касающимся инвестиций промышленной компании в маркетинг нового продукта в отдаленной стране: Сценарий Вероятность Результат Вер. * Рез. Война Кризис Застой Мир Процветание 0,1 0,2 0,2 0,45 Итого: 1,00 -$500 ООО -$200 ООО $0 $500 ООО $1 ООО ООО Ожидание -$50 ООО -$40 ООО $0 $225 ООО $50 000 $185 ООО Заметьте, что это эффективный сценарный спектр, ибо: A. Имеется, по крайней мере, один сценарий с отрицательным исходом. B. Сумма вероятностей равна 1,00. C. Сценарии внутри спектра не пересекаются. Сценарий застоя, например, предполагает мир. Но сценарий застоя предполагает мир с нулевым экономическим ростом. Сценарий мира с ним не пересекается, так как предполагает мир при наличии хоть какого-то экономического роста. Другими словами, сценарий застоя не является частью сценария мира, также как и все другие сценарии по отношению друг к другу. Все сценарии внутри данного спектра должны относиться к исходам одного и того же периода владения. Как уже отмечалось, длительность периода владения может быть любой по вашему усмотрению - это может быть день, неделя, десять дней, месяц, год - все, что угодно, но ее нужно выбрать заранее. Как только это сделано, всем сценариям данного спектра следует сопоставить их возможные исходы в следующем периоде владения, и все сценарные спектры должны соответствовать периодам владения одинаковой длительности. Это имеет решающее значение. Так, если вы остановитесь на одном дне, то все сценарии всех сценарных спектров должны соответствовать возможным исходам следующего дня. Далее мы покажем, как определить оптимальное размещение средств в случае нескольких сценарных спектров, которые одновременно используются в торговле. Данный результат является развитием моей ранней работы об оптимальном f и опционах. Для этого нам потребуется ознакомиться с условными вероятностями. Но сначала мы приведем некоторые подготовительные сведения. Дополнение первое Сокращение дефицита за счет увеличенной дисперсии Валового Внутреннего Продукта в номере Wall Street Joumal за 25 марта 1993 г. опубликована весьма интересная редакционная статья У. Курта Хаузера. По сути, в ней утверждалось, что, несмотря на изменения налоговых ставок и налогового законодательства в послевоенный период, доля ВВП, приходящаяся на собранные налоги (в США), стабилизировалась на среднем значении 19,5%. Кроме того, разброс около этого среднего был относительно невелик и составлял на максимуме в 21,1% (1981г.) и на минимуме - 17,9% (1964-65 гг.). Автор представил весьма убедительные доводы в пользу необходимости более высоких темпов прироста ВВП по сравнению с увеличением правительственных расходов. Отсюда следует, что клинтоновское налоговое послание 1993 г. бьшо некорректно в том смысле, что более стимулирующим для ВВП является вовсе не повышение налогов, как утверждалось, а их понижение. Согласно утверждению м-ра Хаузера, к сокращению дефицита ведет не повышение налоговых ставок, а увеличение ВВП. Похоже, что эта идея имеет широкую поддержку. Однако сокращения дефицита можно достичь, увеличивая дисперсию ВВП, причем столь же эффективно, как за счет увеличения самого ВВП! Эта идея бросает вызов не только обьщенному, но и политическому мьшшению. Общий дефицит представляет собой экспоненциально растущую функцию. Чем больше становится дефицит, тем больше проценты по нему. Покрывая определенную часть процентов по дефициту, то есть капитализируя некоторую часть этих процентов обратно в дефицит, мы создаем (точнее, позволяем нашему правительству создавать) экспоненциально растущую функцию общего дефицита. У всех функций с экспоненциальным ростом имеется некоторое значение / которое можно им сопоставить. Но как нам изменять это значение /, с которым мы (т. е. правительство) действуем? Федеральное правительство неосознанно вырабатывает определенное значение для / Тем не менее, имеется определенное значение /, которое воздействует на него (на всех нас), признаем мы это или нет. Где бы ни находилось федеральное правительство (т. е. мы) на кривой /, мы можем видеть, что сможем извлечь пользу из такого значения /, которому не соответствует вершина кривой. На определенном значении вне вершины, где TWR опускается ниже 1, мы можем получить огромный выифыш, ибо на этом значении мы имеем гарантию того, что функция роста будет сломана. То есть на значении /, где TWR становится меньше 1, мы достоверно знаем, что разорились бы, будь мы игроками с таким значением / Поэтому, если никто не знает, какое значение / мы используем, и при условии, что какое бы значение / ни использовалось де-факто, мы можем выгадать, смещая значение/ближе к 1 (если мы действительно находимся не на вершине кривой). Как можно этого добиться? Мы концентрировались на А, общих государственных доходах. То есть мы акцентировали на увеличении доходов (или сокращении расходов). Однако при этом очень мало внимания бьшо уделено дисперсии этих доходов. Если, согласно идее м-ра Хаузера (а я верю в его правоту), доходы прямо связаны с ВВП (более, чем налоговое законодательство), то можно утверждать кое-что весьма существенное относительно дисперсии ВВП. В конечном счете то, что мы должны сократить, - это G, или коэффициент прироста за период значений HPR федерального дефицита. По теореме Пифагора противостоящие компоненты формулы для оценки среднего геометрического, этого можно достичь не только увеличением А, средних доходов (рши среднего ВВП), но также и путем увеличения S, стандартного отклонения или дисперсии доходов (стандартного отклонения или дисперсии ВВП, согласно данным из статьи Хаузера)! Так, увеличение дисперсии ВВП уменьшает скорость роста федерального дефицита на величину, которая больше эквивалентного увеличения в арифметическом среднем ВВП! При увеличении / от О до 1 изменяются и стандартное отклонение, и арифметическое среднее значений HPR. При нулевом /стандартное отклонение (или его квадрат - дисперсия)
|