

 |
 |
|
Факторинг Управлению капиталом Но что мы будем использовать в качестве весов W1 и W2? Как оказывается, W1 равен 1 минус абсолютная величина коэффициента корреляции: W1 = (1 - И). А W2 есть просто абсолютная величина коэффициента корреляции: W2 = И. Эта весовая схема гарантирует нам, что мы останемся в пределах верхних и нижних границ. Так, когда г = О, наше уравнение целиком склоняется в пользу произведения двух вероятностей, а когда И = 1, перевес будет целиком в пользу интерантисечения. Полностью уравнение для аппроксимации совместных вероятностей имеет вид: P(Pi IPz) = Pi *Р2 * (1 - И) + ДР, *Р2) * И- Мы называем функцию линейно взвешенной (т. е. ни один из ее аргументов не имеет степени большей единицы), так как ее графиком служит прямая линия. Мы можем убедиться в линейности соотношений между р, * ри /(р, * р), наблюдая за следующими двумя потоками исходов бросания монеты: Поток! ОООООРРРРР Поток2 ООООРОРРРР ВРЕМЯ Если приглядеться к этим двум потокам, то мы увидим, что в каждом из них вероятность исхода О и исхода Р равна 0,5. Подсчитав коэффициент корреляции между этими потоками, получим 0,6. Далее, для г = О получаем р, * Pj = 0,5 * 0,5 = 0,25. Если нас интересует выпадение орлов в обоих потоках одновременно, то получаем интерантисечение /(Pj * р), равное 0,5: Монета Монета 2 Решка Решка Если коэффициент корреляции больше О, то мы не разворачиваем сценарный спектр на 180 градусов. Заметьте, что, когда нас интересует интерантисечение обоих потоков, одновременно дающих решку, получим, что его величина также равна 0,5. При г = О имеем, что совместная вероятность выпадения обоих орлов равна р * р (или, как в данном случае, и для обеих решек). При г = 1 имеем совместную вероятность, равную ин-терантисечению 0,5. При г = - 1 интерантисечение бьшо бы равно О, а, значит, и совместная вероятность равна О, как явствует из следующего рисунка. Монета 1 Монета 2 Решка Орел Interontisection is О Таким образом, получаем следующие три точки, в которых мы уверены: Вероятность 0,25 0,5 Изобразим эти три точки на графике (см. рис. 3.2.). Мы видим, что эти три точки можно соединить прямой линией. Впрочем, их можно соединить и какой-нибудь кривой О 0,5 -Q О -Q О 0.1 0.05
Рис. 3.2. (т. е. функция не будет линейно взвешенной), например сигмо-идой (т. е. растянутой S-образной кривой, проходящей через наши три точки). Итак, в обоих потоках орел выпат четыре раза из десяти (анатогично, решка выпата в обоих потоках четыре раза из десяти), что дает вероятность 0,4. Обратите внимание, что если функция линейна, то есть изображается на графике прямой линией, то эта прямая проходит через точку, соответствующую коэффициенту корреляции 0,6 и вероятности 0,4. Если бы график функции отличатся от прямой, то коэффициенту корреляции 0,6 соответствовало бы все, что угодно, кроме 0,4! (см. рис. 3.3). Теперь рассмотрим нашу функцию применительно к этим двух потокам исходов: РСцз) = Pi * Рг * (1 - И) + Д?! * Рг) * И = 0,5 * 0,5 * (1 - 0,6) + 0,5 * 0,6 = 0,25.0,4 + 0,5.0,6 = 0,1 + 0,3 = 0,4 То есть мы видим, что наша формула дает такой результат, который подтверждается самим потоком исходов. Мы можем ожидать появления орлов в обоих потоках одновременно с вероятностью 0,4, при бросании двух идеальных монет с коэффициентом корреляции г = 0,6. -Q О -Q О -0.5 0.45. -0.4 0.35 0.3 0.2! -0.1 0.05 -О -0.5 О 0.5 Correlation coefficient Рис. 3.3. Совместные вероятности линейно взвешены с помощью коэффициента корреляции. Эта аппроксимация проходит только в случае биномиального распределения (т. е. при двух сценариях в спектре). Чем более уклоняются вероятности от 0,5 на сценарий, тем менее точной она становится. Другими словами, это решение является точным, когда вы дихотомизируете два сценарных спектра; в противном случае она превращается в аппроксимацию убывающей точности. Впрочем, любые сценарные спектры можно свести к биномиальным распределениям (наборам только из двух сценариев), путем дихотомизации около их центров. Вновь обратимся к сценарному спектру нашей промышленной компании. Он содержит восемь различных сценариев. Мы можем дихотомизировать их, объединив воедино сценарии Войны, Кризиса и Стагнации в один сценарий нового сценарного спектра, который мы будем называть сценарием Плохой половины исходов. Аналогичным образом, мы можем объединить воедино сценарии мира и процветания в сценарий Хорошей половины исходов нового спектра. Теперь мы можем обращаться с преобразованным спектром так же, как и с другими спектрами, содержащими по два сценария, и аппроксимировать совместные вероятности четырех возможных совместных исходов (рис. 3.4). Дихотомизация сценарных спектров для аппроксимации совместных вероятностей эффективна лишь до тех пор, пока вы разделяете их примерно на равновероятном уровне (0,5). Чем дальше от него проводится дихотомизация, тем менее точной становится аппроксимация.
Рис. 3.4. Вновь обратимся к примеру из Феллера, приведенного в начале этой главы: Безусл. плотность Y 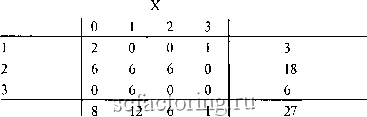 Безусл. плотность X Если дихотомизировать сценарный спектр X, объединив исходы О и 1 в сценарий А спектра X, а исходы 2 и 3 в сценарий В спектра X, то мы удалимся от равновероятного уровня. Уровень, который мы получим при такой дихотомизации, будет равен 0,74074, поскольку, судя по безусловным плотностям в X, двадцать из двадцати семи исходов (74,074%) приходятся на О или 1, и только семь из двадцати семи исходов (25,92%) приходятся на 2 или 3 (см. рис. 3.5). Если то же самое проделать со сценарным спектром У, объединяя исходы 1 и 2 в сценарий А спектра Y, а исход 3 переименовывая в сценарий В спектра Y, то преобразованный спектр Y станет таким, как показано на рис. 3.6. Заметьте, что спектр Y также дихотомизирован не равновероятно, а поблизости к 0,777. Приступим к формированию таблицы совместных вероятностей в следующем виде:
0,296 0,74074 0,9629 1,0 Рис. 3.5. Дихотомизация безусловной плотности X.
о 0,111 0,777
Рис. 3.6. Дихотомизация безусловной плотности Y. Теперь, исходя из того, что коэффициент корреляции г между этими двумя сценарными спектрами равен О, определим четыре совместные вероятности нащей таблицы: р{А 1 А) = 0,74074 * 0,777 * (1 - 0) + 0,74074 * О = 0,5761; р{А I В) = 0,74074 * 0,222 * (1 - 0) + О * О = 0,16461; 0,5 0,95 1,0
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||