

 |
 |
|
Факторинг Управлению капиталом Давайте рассмотрим еще один пример. Предположим, что мы бросаем три монетки по 10 центов и три монетки по 25 центов. Пусть в сценарный спектр А входят общее количество орлов на всех шести монетах, а в сценарный спектр В - общее количество орлов только на 25-центовиках. Таблица совместных вероятностей будет иметь вид:
Всего здесь имеется 2 (64) различных исходов, а коэффициент корреляции составляет 0,707 (рис. 3.7). Поэтому, если мы 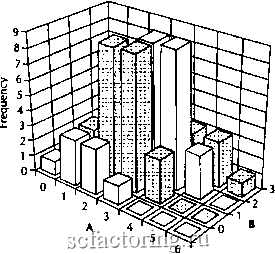 Рис. 3.7. Пример совместного распределения исходов бросания трех 10-центовиков и трех 25-центовиков. хотим определить совместные вероятности, ассоциированные с А = 2 и В = 1 (т. е. вероятность при бросании всех шести монет получить два или менее орлов среди всех шести монет и не более одного орла среди 25-центовиков), то: р(<=2<=1) = ((15 + 6 + 1)/64) * ((8 + 24)/64) * * (1 - I 0,707 I) + ((15 + 6 + 1)/64) * I 0,707 =(22/64) * (32/64) * 0,293 + (22/64) * 0,707 =0,34375 * 0,5 * 0,293 + 0,37375 * 0,707 =0,050359375 + 0,26424125 =0,314600625. Что при умножении на 64 (общее число исходов) дает в данном квадранте ожидание, равное 20,1344 исходам. Мы же знаем, что в этом квадранте имеется 19 исходов. Обратите внимание, что, хотя мы и дихотомизировали В на уровне 0,5, мы не дихотомизировали А. Отсюда расхождения наших результатов с эмпирическимим данными. Если бы мы и А дихотомизировали на уровне 0,5, то ползили бы совершенно точный результат. После дихотомизации таблицы мы можем взять одну из ее новых частей и дихотомизировать ее при условии, что известен коэффициент корреляции этой новой таблицы. Поэтому, если бы мы захотели дихотомизировать верхний левый квадрант этой таблицы, то не смогли бы использовать 0,707 в качестве коэффициента корреляции. Нам пришлось бы определить (или оценить) коэффициент корреляции только для такого набора данных, где при бросании наших шести монет выпадают не более двух орлов на всех монетах и не более одного орла на 25-центовиках. Таким образом, при наличии двух сценарных спектров и коэффициента (ов) корреляции между ними мы можем определить совместнью вероятности реализации двух сценариев, по одному из каждого спектра. Тот, КТО следует среднедисперсионному подходу, или старой методологии, опирается в основном на совместные распределения, у которых только четыре квадранта, - так уж они используют коэффициент корреляции в качестве меры взаимозависимости компонентов. Это плохо приближает реальные совместные распределения, что еще раз подчеркивает предпочтительность нащей новой методологии по сравнению со старыми подходами. Совместные вероятности двух непрерывных распределений Сценарные спектры можно представлять себе как дискретные распределения. Такой же подход можно использовать и для определения вероятностей для непрерывного распределения, если рассматривать его как дискретное распределение с бесконечно малым щагом квантования (т. е. с бесконечным множеством сценариев). Например, мы знаем, что центрированная нормально распределенная случайная величина с вероятностью 0,9772 не превышает двух стандартных отклонений, а с вероятностью 0,9986 - трех стандартных отклонений. Если один из сценариев спектра состоит в том, что нормально распределенная случайная величина попадает в пределы от +2 до +3 стандартных отклонений, то мы знаем, что вероятность этого сценария равна 0,0214 (0,9986 -0,9772). Значит, мы можем определять совместные вероятности для непрерывных распределений. Кроме того, мы можем сделать сценарий таким маленьким, как нам нужно. В упомянутом ранее примере мы можем использовать сценарий, который состоит в том, что нормально распределенная случайная величина попадает в пределы от +2 до +2,1 стандартных отклонений, или между +2 и +2,000001 стандартных отклонений. Изложенный метод поквадрантной оценки совместных распределений вероятности при известных безусловных плотностях и коэффициенте корреляции между ними весьма привлекателен. Он точно описывает механизм формирования совместного распределения из компонентных безусловных распределений. Когда мы используем распределение Бернулли (распределение, у которого только два возможных исхода, т. е. сценарные спектры состоят только из двух сценариев), можно получить очень хорошую и простую оценку совместньгх вероятностей. Но чтобы сделать ее еще точнее, т. е. найти более детальные совместные вероятности, не ограничиваясь на квадрантах, требуется наперед знать коэффициенты корреляции составляющих квадрантов (или наперед знать совместные вероятности, чтобы, обратив формулу, получить коэффициенты корреляции). При наличии зависимости совместные распределения будут изменяться под влиянием непосредственно предшествующих исходов. Нередко нам будут известны не все коэффициенты корреляции между двумя сценарными спектрами, и поэтому мы будем вынуждены получить недостающие данные либо эмпирическим путем, либо с помощью оценки. Если у вас имеются необходимые эмпирические данные, то рассчитать совместные вероятности совсем не сложно. Предположим, например, что вас интересуют совместные вероятности для двух акций - корпораций XYZ и АБС. У вас есть масса различных сценариев ожидаемого поведения цены каждой из них на следующий период владения (а период владения может быть любой единой длины по нашему выбору - это может быть день, два дня, неделя, месяц, год - что угодно). Один из сценариев спектра ЛВС соответствует подъему цены ее акций на два пункта. У вас также есть сценарий из спектра XYZ, соответствующий падению цены ее акций на полпункта. (Вместо абсолютных величин можно использовать изменения цены в процентах.) С помощью компьютера можно просчитать ценовые данные по обеим Оценка совместных вероятностей этим акциям и подсчитать, в скольких периодах владения акции ABC поднимались на два пункта, а акции XYZ - опускались на полпункта, и поделить полученную величину на общее количество периодов владения анализируемого массива данных. Затем мы можем проделать то же самое для каждой комбинации двух сценариев из наших сценарных спектров. То есть мы бы получили таблицу совместных вероятностей двух сценарных спектров эмпирическим путем. Разумеется, располагая эмпирическими данными, можно сначала рассчитать требуемые коэффициенты корреляции, а затем на их основе построить таблицу совместных вероятностей. Мы можем также оценить величины входящих в таблицу совместных вероятностей двух сценарных спектров. Делая это, нужно помнить о верхних и нижних границах каждой совместной вероятности, чтобы наши оценки не вышли за их пределы. Нижняя граница совместной вероятности, как вы помните, равна 0. Верхняя граница равна минимуму из двух индивидуальных вероятностей. Кроме того, нужно, чтобы сумма всех совместных вероятностей в таблице строго равнялась 1,0. Вспомните также, что каждая строка и каждый столбец таблицы совместных вероятностей двух сценарных спектров должны в сумме давать безусловную вероятность этой строки или столбца. Например, рассмотрим два различных сценарных спектра: Спектр Y
Война Кризис Стагнация Мир Процветание Безусловная Плотность У  Безусловная Плотность X 0,45 0,05 Из этого примера видно, что сумма вероятностей в первом столбце должна равняться безусловной плотности, ассоциированной со столбцом Хорошие исходы (0,4). То есть сумма совместных вероятностей Войны , Кризиса , Стагнации , Мира и Процветания , с одной стороны, и Хороших исходов , с другой - должна быть строго равна 0,4. Аналогично, сумма вероятностей в первой строке, то есть совместная вероятность Хороших исходов и Войны плюс совместная вероятность Плохих исходов и Войны , должна равняться величине, ассоциированной с этой строкой, то есть с Войной (0,1). Если взять последнюю строку Процветание , то суммарно Хорошие исходы с Процветанием и Плохие исходы с Процветанием должны давать 0,5. Заметьте, что если потребовать, чтобы совместные вероятности в каждой строке и в каждом столбце суммарно равнялись безусловной плотности, ассоциированной с каждой строкой и каждым столбцом (как и должно быть), то уже не нужно будет беспокоиться о том, чтобы ни одна совместная вероятность не превысила бы верхней границы (и, пока все ваши совместные вероятности больше или равны О, как это и положено, не нужно беспокоиться о пересечении ими нижней границы). Кроме того, если совместные вероятности в каждой строке и в каждом столбце равны безусловным плотностям, ассоциированным с каждой строкой и каждым столбцом, то Исходя из этого, строим таблицу:
|