стающим числом желающих присоединиться к движению, направление которого уже определилось с достаточной очевидностью.

В условиях подобной убежденности больщинства в своей правоте волна 3 должна быть особенной с точки зрения размаха и скорости движения. И чаще всего по длине пробега она бьшает максимальной из всех волн импульсной стадии цикла.

Однако эмпирические данные убедили Эллиотта в том, что такое происходит не всегда. Зато всегда справедливо другое положение: волна 3 не может быть самой короткой из всех трех импульсных волн пятиволновки данного цикла, т.е. она либо самая длинная, либо средней длины (рис. 3-6).

Отметим также, что эта аксиома не отрицает возможность существования волны 3, равной по длине другим импульсным волнам этой же стадии данного цикла. Например, на графиках 1, 2 и 4 волна 3 - наибольшая по протяженности (на графиках 1 и 2 - это волна iii), а на графике 3 - примерно равна волне 1 (волна i на графике).*

Волна 3 - вторая по длине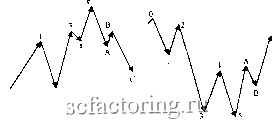

о/ 2

Волна 3 - вторая по длине

Рис. 3-6. Особенности продолжительности волны 3.

Если же при анализе реального движения рынка фиксируется факт нарушения аксиомы (волна 3 оказывается самой короткой), то необходимо пересмотреть маркировку волн. И ту, что имеет номер 3, нужно искать где-то в другом месте.

Хотя иногда для этого придется ждать завершения всей импульсной стадии цикла, другого способа определить ее нет. И с этим приходится мириться.

Как отмечалось выше, выполнение условия аксиомы не означает подтверждения верности маркировки волн. Аксиома, так сказать, работает от противного , т.е. именно тогда, когда фиксируется ее нарушение. Впрочем, если нарушения нет, то не исключено, что возможная ошибка просто пока еще ничем себя не проявила.

См. Приложение.

Если нарушение данной аксиомы - это явное свидетельство неверности принятой разметки волнового движения, то соблюдение ее может говорить лишь о том, что ошибка еще не выявлена.

Непересечение волн 1 и 4. Если образно представить импульс как марш-бросок, а коррекцию - как отступление в движении рынка, то, исходя из представления о мощи волны 3, данная аксиома должна формулироваться следующим образом: после за-вергиения волны 3 откатывающаяся волна коррекции 4 не может отступить (overlap)на территорию, занятую ещев ходе развития волны 1.

Выполнение условия этой аксиомы - показатель перехода, совершенного рынком благодаря высокой энергии движения волны 3, на качественно иной уровень цен.

Как видно на схеме (рис. 3-7), есть две группы непересекающихся волн: 1-2 и 4-5, которые связаны волной 3 (см. также график 4). Данный факт позволяет в любой пятиволновке легко обнаружить признаки импульса.

Но полной определенности здесь нет. Причина та же, что и раньше: выполнение не означает подтверждение. Другими словами, ситуация непересечения не является признаком, гарантирующим, что это именно волна 3. Дело в том, что внешне точно так же может выглядеть и стадия сложной коррекции (рис. 3-8).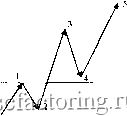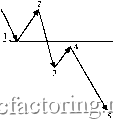

Рис. 3-7. Аксиома о непересечении волн 1 и 4.

В этой связи в качестве дополнительного признака импульс-ности, а не коррекционности движения, иногда предлагается рассматривать удаленность волны 4 от уровня завершения волны 1. Чем больше это расстояние, тем увереннее можно говорить, что события разворачиваются на стадии импульса, а не коррекции.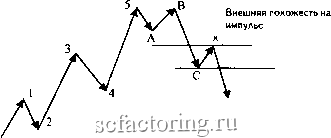

Сложная коррекция

Рис. 3-8. Возможность непересечения между волнвми сложной коррекции .

Дополнительным признаком того, что события разворачиваются на импульсной стадии, может служить значительный размах зоны непересечения волн 1 и 4,

Например, на графиках 1и 2 (см. Приложение) такое удаление достаточно велико (волны i-ii и iii-iv, а волна 4 на графике 4 вплотную приблизилась к запретной зоне - вершине волны 1.

К сожалению, как отмечалось выше, признак удаленности вряд ли может служить критерием, определяющим достаточно точно характер движения.

Тем не менее нарушение аксиомы о непересечении волн 1 и 4 должно настораживать. Например, волна, ошибочно принятая за импульс 3, в действительности может оказаться волной с номером 5. А обозначенная как волна 4 - волной А (рис. 3-9).

Другой пример, в котором вместо 1-2-3-4-5 имеем А-В-С-1-2 и т.д., приведен на рис. 3-10.

Однако некоторые сложности возникают в связи с тем, что данная аксиома предусматривает возможность и вполне законных нарушений.

Не вдаваясь в подробности, ограничимся простым их перечислением.