По вопросу о числовом ряде Фибоначчи и .золотом сечении , имеющем статус универсального закона природы, написано очень много. Те, кто имеет доступ к Интернету, могут провести поиск по сочетанию Fibonacci ratios* и получить необходимую информацию. Применительно к тре11дипгу интерес может представлять монография Роберта Фишера (Robert Fisher. Fibonacci Apphcations and Strategies for Traders), Исчерпывающий обзор по данному вопросу дан в книге Роберта Пректера (Robert R. Prechter, jr. Wave Principle of Human Social Behavior and the New Science of Socionomics).

сценариев для пространственно-временных соотношений и пропорций между волнами рассматриваемого цикла.

Положения о тяготении соотношений и пропорций между отдельными волнами и стадиями цикла к хорошо известным коэффициентам золотого сечения составляют отдельную подгруппу правил-тенденций волнового принципа*.

Основная практическая сложность в том, что заранее невозможно сказать, какой из сушествуюшего множества золотых коэффициентов реализуется в конкретном случае.

При вычислении пропорций между волнами цикла наиболее вероятным событием будет появление различных коэффициентов золотого сечения . Однако при этом полностью неопределенным остается то, какой из них будет выбран рынком в каждом отдельном случае.

Итак, каждая из волн, которые развиваются в пространственно-временной плоскости, имеет две соответствующие координаты измерения:

пространственную ( пробег в принятых единицах);

временную (число единиц используемого масштаба, уходящих на создание данной волны).

При этом соотношения между ними тяготеют к тем или иным коэффициентам золотого сечения .

Согласно волновому принципу, расчет заключается в том, чтобы возможные координаты волн оценивать путем надлежащего взвешивания разных пропорций, которые возникают между отрезками движения.

В настоящее время можно говорить как минимум о трех направлениях, в рамках которых предлагается делать те или иные расчеты, необходимые для формулировки прогнозных суждений.

Прежде всего, это измерение пространственного пробега волн одного и того же цикла с последующим анализом возникающих

между ними соотношений. Единицей измерения может быть текущая биржевая (или внебиржевая ) цена в привязке к месту торгов либо некий синтетический показатель - котировка, подобно тому, что имеет место на мировом валютном рынке.

Другое направление - использование только временного параметра. Здесь в качестве отрезков для расчета пропорций берутся те промежутки времени, которые занимает движение рынка между некими экстремальными значениями.

Наконец, в рамках третьего направления, которое мы представим, предпринимается попытка иметь дело с таким показателем, как занимаемая волной условная площадь . Это есть произведение пространственного пробега на время, которое на него уходит. Анализу подвергаются именно отношения между, так сказать, пространственно-временными площадями соответствующих волн.

Движение в пространстве

Представим себе движение против часовой стрелки (или в обратном направлении) через точки а, Ь, с, d и т.д., которые соединяют перпендикулярно расположенные отрезки. Пусть при этом каждый последующий отрезок будет больше предыдущего на некую постоянную в процентном отношении величину. В результате возникает нечто, похожее на спираль, характеристики которой будут меняться в зависимости от установленных между отрезками пропорций (рис. 5-52).

Наиболее привлекательно выглядят спирали с фиксированной пропорцией, т.е. построенные на отрезках, подчиняющихся следующему правилу:

(Оа): (аЬ) = (аЬ): (be) = (be): (cd) = (cd): (de) = (de): (eO и т.д.

Однако ощущение полной гармонии появляется только при определенном значении данного соотношения. Это иррациональное число заслуженно получило название золотого сечения . Если брать его с точностью до трех знаков, то оно представляет собой внешне ничем не примечательное сочетание цифр - 0,618 (или 1,618) в зависимости от того, в каком направлении двигаться по спирали: на расширение или на сжатие .

Золотое сечение можно по праву считать магическим.

Прежде всего, это единственное число, которое дает один и тот же результат при таких противоположных операциях с единицей, как деление и сложение:

1:0,618 = 1 + 0,618.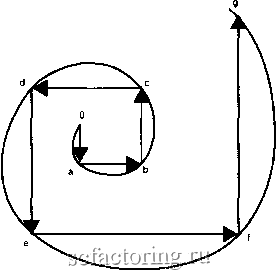

Рис. 5-52. Движение по спирали.

Кроме того, оно настойчиво возникает и при ряде других математических действий:

1 - 0,618 = 0,6182; 0,618 - 0,6182 = 0,6183; 0,6182 0,6183 = 0,618 и т.д.

К слову сказать, именно к этому предельному значению стремится отношение двух соседних членов ряда Фибоначчи:

0,1,0-И = 2,2-н1=3,3-н2 = 5,5-нЗ = 13,13-8 = 21 и т.д.

;-н5 =

Данный предел можно увеличивать или уменьшать в пропорции, равной самому золотому сечению . Тогда увеличение даст такие цифры:

1,618 X 1,618 = 2,618; 2,618 X 1,618 = 4,236; 4,236 X 1,618 = 6,854 и т.д.