Длина mO меньше 38,2% длины ml Jj.4a

38,2% длины ml----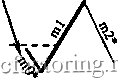

Правило 4а (П-4а)

38,2% длины ml -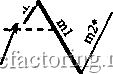

Длина mO меньше 38,2% длины ml 11-4а

Правило 4Ь (П-4Ь)

Длина тО не меньше 38,2%, но меньше 100% длины ml

100% длины ml

38,2% длины ml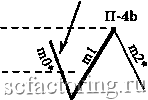

38,2% длины ml---- /

100% длины ml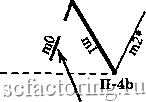

Длина тО не меньше 38,2%, но меньше 100% длины ml

Длина тО не меньше 100%, но меньше 161,8% длины ml

Правило 4с (П-4с)

161,8% длины ml---

100% длины ml---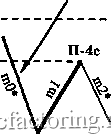

100% длины ml -161,8% длины ml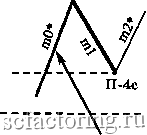

Длина тО не меньше 100%, но меньше 161,8% длины ш1

Правило 4d (n-4d)

Продолжение Рисунка 3-27 на следующей странице

261,8% длины ml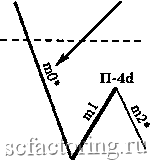

Длина тО должна лежать в пределах 161,8-261,8% (включительно) длины ml

161,8% длины ml

* mO и m2 на всех диаграммах этой страницы могут состоять из 1, 3, 5 или более моноволн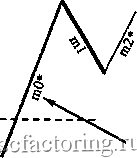

n-4d

161,8% длины ml

Длина тО должна лежать в

пределах 161,8-261,8% (включительно) длины ml

261,8% длины ml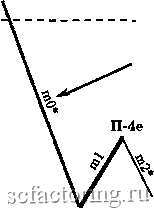

261,8% длины ml

Длина тО должна быть больше 261,8% длины ml

* Может состоять из 1, 3, 5 и более моноволн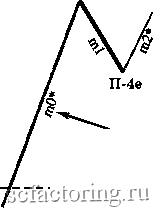

Длина тО должна быть больше 261,8% длины ml

261,8% длины ml

Правило 5 (длина т2 не меньше 100%, но меньше 161,8% длины ml)

Чтобы Правило 5 вступило в действие, длина т2 должна быть не меньше 100%. но меньше 161.8% длины ml (см. Рисунок 3-28). Если это верно, вычислите отношение длины тО к длине ml. Затем, сверившись с приведенным ниже списком, определите, какое Условие Правила 5 действует в данном случае.

Рисунок 3-28

Длина тО может быть любой, от 0%

до более 261,8% , длины волны ml

Правило 5 (П-5)

(условия применения)

161.8%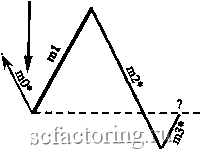

* Может состоять из 1, 3, 5 и более моноволн

100%

161.8%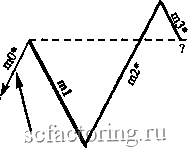

- 100%

Длина тО может быть любой, от 0%

до более 261,8% длины волны ml

Условия Правила 5

Условие а : если длина тО меньше 100% длины ml, применяется Правило 5а; отметьте это на графике у конечной точки ml (переходите к Правилу 5, Условию а Неформальных Правил логики *);

Условие Ъ : если длина тО не меньше 100%, но меньше 161,8% длины ml, в силу вступает Правило 5Ь (переходите к Правилу 5, Условию Ь Неформальных Правил логики *);

Условие с : если длина тО лежит в пределах 161.8-261.8% длины ml (включительно), применяется Правило 5с (переходите к Правилу 5, Условию с Неформальных Правил логики *);

Условие d : если длина тО больше 261.8% длины ml, имеют место уникальные обстоятельства Правила 5d, рассмотренные ниже (переходите к Правилу 5, Условию d Неформальных Правил логики *).

Правило 6 (длина m2 лежит в пределах 161,8%-261,8% длины ml [включительно])

Чтобы Правило 6 вступило в действие, длина т2 должна лежать в пределах 161,8-261,8% длины ml, включительно (см. Рисунок 3-29). Затем вычислите отношение длины тО к длине ml и, сверившись с приведенным ниже списком, решите, какое Условие Правила 6 действует в данном случае.

Рисунок 3-29

261,8% длины ml

* Может состоять из 1, 3, 5 и более моноволн

Длина тО может быть любой, от 0% до более 261,8% длины волны ml

161,8% длины ml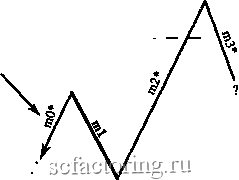

Длина тО может быть любой, от 0% до более 261,8% длины волны ml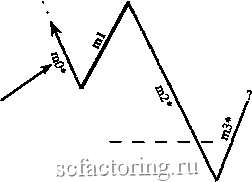

161,8% длины ml

Правило 6

(условия применения)

261,8% длины ml

Условия Правила 6

Условие а : если длина тО меньше 100% длины ml, должно применяться Правило 6а (переходите к Правилу 6, Условию а Неформальных Правил логики *);

Условие Ь : если длина тО не меньше 100%. но меньше 161.8% длины ml, в силу вступает Правило 6Ь (переходите к Правилу 6, Условию Ь Неформальных Правил логики *);

Условие с : если длина тО лежит в пределах 161.8-261.8% длины ml (включительно), применяется Правило 6с (переходите к Правилу 6, Условию с Неформальных Правил логики *);

Условие d : если длина тО больше 261.8% длины ml, применяется Правило 6d (переходите к Правилу 6, Условию d Неформальных Правил логики *).

* Неформальные Правила логики начинаются на странице 3-32

Правило 7 (длина т2 больше 261,8% длины ml)

Чтобы Правило 7 вступило в действие, длина т2 должна быть больше 261.8% длины ml (см. Рисунок 3-30). Затем вычислите соотношение длин тО и ml, изучите приведенный ниже список и решите, какое из Условий Правила 7 действует в данном случае (также см. Рисунок 3-30 на следующей странице).